Fiche de mathématiques
Ile mathématiques > maths bac > Bac 2023 toujours : des sujets venus d'ailleurs
Bac Mathématiques
Durée : 3h
Coefficient: 3
Calculatrice non autorisée
5 points
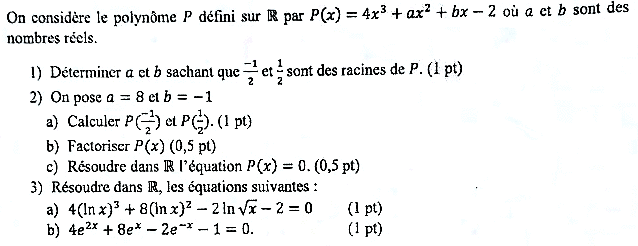
6 points
9 points
1) On a=4x^3+ax^2+bx-2 )
.
Puisque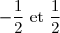
sont des racines de 
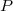, alors:
=0 \\ P\left(\dfrac{1}{2}\right)=0\end{cases} &\iff& \begin{cases} 4\left(-\dfrac{1}{2}\right)^3+a\left(-\dfrac{1}{2}\right)^2+b\left(-\dfrac{1}{2}\right)-2=0 \\ 4\left(\dfrac{1}{2}\right)^3+a\left(\dfrac{1}{2}\right)^2+b\left(\dfrac{1}{2}\right)-2=0 \end{cases} &\iff& \begin{cases} -\dfrac{4}{8}+\dfrac{a}{4}-\dfrac{b}{2}-2=0 \\ \dfrac{4}{8}+\dfrac{a}{4} +\dfrac{b}{2}-2=0\end{cases} \\\\ &\iff& \begin{cases} \dfrac{-2+a-2b}{4}=2 \\ \dfrac{2+a+2b}{4}=2\end{cases} &\iff& \begin{cases} a-2b=10 \\a+2b=6\end{cases} \\\\ &\iff& \begin{cases} a=10+2b \\4b=-4 \end{cases} &\iff& \boxed{\begin{cases} a=8\\ b=-1\end{cases} }\end{matrix} )
2-a) On a trouvé que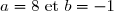
si et seulement si 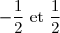sont des racines de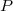
Donc, directement:=P\left(\dfrac{1}{2}\right)=0})
b) Puisque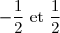 sont des racines de 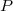, alors il existe 
:
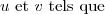=\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)(ux+v) &\iff& 4x^3+8x^2-x-2 =\left(x^2-\dfrac{1}{4}\right)(ux+v) \\\\&\iff& 4x^3+8x^2-x-2 = ux^3+vx^2-\dfrac{u}{4}x-\dfrac{v}{4} \\\\&\iff& \begin{cases} u=4 \\ v=8 \\\dfrac{u}{4}=1 \\ \dfrac{v}{4}=2 \end{cases} \\\\&\iff& \boxed{\begin{cases} u=4 \\ v=8 \end{cases}}\end{matrix} )
Donc:
=\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)(4x+8)\iff \boxed{ P(x)=4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)(x+2)} )
c) Résolvons l'équation=0\text{ : })
=0 &\iff& 4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)(x+2)=0 \\&\iff& x-\dfrac{1}{2}=0 \text{ ou }x+\dfrac{1}{2}=0\text{ ou }x+2=0 \\&\iff& x=-\dfrac{1}{2}\text{ ou }x=\dfrac{1}{2}\text{ ou }x=-2 \end{matrix} )
=0 \text{ est : }S=\left\lbrace -2;-\dfrac{1}{2};\dfrac{1}{2}\right\rbrace })
3-a) Résolvons l'équation^3+8(\ln x)^2-2\ln \sqrt{x} -2=0\text{ : })
^3+8(\ln x)^2-2\ln \sqrt{x} -2=0&\iff& 4(\ln x)^3+8(\ln x)^2-\ln \sqrt{x}^2 -2=0\\ &\iff& 4(\ln x)^3+8(\ln x)^2-\ln x -2=0 \\&\iff& 4X^3+8X^2-X-2=0 \enskip\enskip\enskip \text{(En posant: }X=\ln x\text{)} \\&\iff& X=-\dfrac{1}{2}\text{ ou }X=\dfrac{1}{2}\text{ ou }X=-2 \\&\iff& \ln x=-\dfrac{1}{2}\text{ ou }\ln x=\dfrac{1}{2}\text{ ou }\ln x=-2 \\&\iff& x=e^{-\frac{1}{2}}\text{ ou }x=e^{\frac{1}{2}}\text{ ou }x=e^{-2}\end{matrix} )
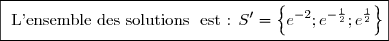
b) Résolvons l'équation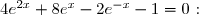
=0\times e^x\\ &\iff& 4e^{3x}+8e^{2x}-2-e^x=0 \\&\iff& 4\left(e^x\right)^3+8\left(e^x\right)^2-e^x-2=0 \\&\iff& 4X^3+8X^2-X-2=0 \enskip\enskip\enskip \text{(En posant: }X=e^x\text{)} \\&\iff& X=-\dfrac{1}{2}\text{ ou }X=\dfrac{1}{2}\text{ ou }X=-2 \\&\iff& e^x=\dfrac{1}{2}\enskip\enskip \text{ (car pour tout réel }x\text{ : }e^x>0\text{)} \\&\iff& x=\ln \dfrac{1}{2} \\&\iff& x=-\ln 2\end{matrix} )
On note
1-a) Directement d'après l'énoncé:
Si le joueur obtient\text{ , alors : }X=-500)
Si le joueur obtient\text{ ou }(F;P)\text{ , alors : }X=100)
Si le joueur obtient\text{ , alors : }X=200)
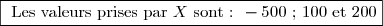
b) Dressons un arbre pondéré:
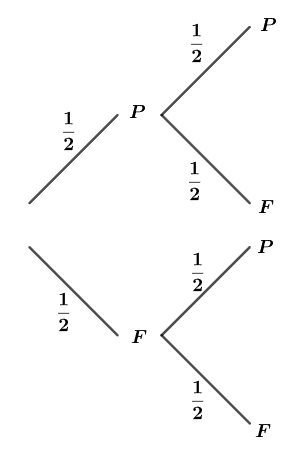
On a donc:
=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4})
=\dfrac{1}{2}\times \dfrac{1}{2}+\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2})
=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4})
Et on représente la loi de probabilité de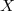
sous forme de tableau:
 &\dfrac{1}{4}&\dfrac{1}{2}&\dfrac{1}{4} \\ &&&\\ \hline \end{array})
c) Calculons l'espérance mathématique})
de .
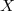=\displaystyle\sum_{i=1}^3x_i\,P(X=x_i)=-500\times \dfrac14+100\times\dfrac12+200\times\dfrac14 \Longrightarrow\quad\boxed{E(X)=-\dfrac14})
d) L'espérance mathématique est négative, donc:
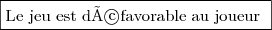
2-a) Directement d'après l'énoncé:
Si le joueur obtient\text{ , alors : }Y=-500)
Si le joueur obtient\text{ ou }(F;P)\text{ , alors : }Y=a)
Si le joueur obtient\text{ , alors : }Y=2a)
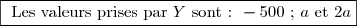
b) De la même manière, et en utilisant le même arbre pondéré, on trouve:
=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4})
=\dfrac{1}{2}\times \dfrac{1}{2}+\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2})
=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4})
Et on représente la loi de probabilité de
sous forme de tableau:
 &\dfrac{1}{4}&\dfrac{1}{2}&\dfrac{1}{4} \\ &&&\\ \hline \end{array})
c) Calculons l'espérance mathématique})
de .
=\displaystyle\sum_{i=1}^3y_i\,P(Y=y_i)=-500\times \dfrac14+a\times\dfrac12+2a\times\dfrac14 \Longrightarrow\quad\boxed{E(Y)=\dfrac{-500+4a}{4}})
3) Le jeu est équitable si et seulement si l'espérance mathématique est nulle, donc:
=0&\iff& \dfrac{-500+4a}{4}=0&\iff& -500+4a=0 &\iff& a=\dfrac{500}{4} &\iff& \boxed{a=125}\end{matrix})
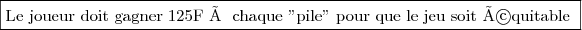
Partie A:
![\forall x\in]0;+\infty[\text{ : }g(x)=x^2-2\ln x](https://latex.ilemaths.net/latex-0.tex?\forall x\in]0;+\infty[\text{ : }g(x)=x^2-2\ln x)
1)
La limite en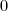
à droite:
 &=& \displaystyle\lim_{x\to 0^+}x^2-2\ln x &=& 0-2\times (-\infty) &=& +\infty \end{matrix} )
La limite en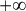
:
![\begin{matrix} \displaystyle\lim_{x\to +\infty}g(x) &=& \displaystyle\lim_{x\to +\infty}x^2-2\ln x &=& \displaystyle\lim_{x\to +\infty}x\left(x-2\dfrac{\ln x}{x}\right)&=& (+\infty)\times \left[(+\infty)-2\times 0\right] &=& +\infty \end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} \displaystyle\lim_{x\to +\infty}g(x) &=& \displaystyle\lim_{x\to +\infty}x^2-2\ln x &=& \displaystyle\lim_{x\to +\infty}x\left(x-2\dfrac{\ln x}{x}\right)&=& (+\infty)\times \left[(+\infty)-2\times 0\right] &=& +\infty \end{matrix} )
Conclusion:
=+\infty\enskip\text{ et }\enskip \displaystyle\lim_{x\to +\infty}g(x)=+\infty})
2-a) La fonction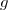
est dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[)
comme somme de fonctions dérivables sur cet intervalle.
![\begin{matrix} \forall x\in]0;+\infty[\text{ : } g'(x)&=&\left(x^2-2\ln x\right)'&=& 2x-2\times \dfrac{1}{x}\\\\ &=& \dfrac{2x^2-2}{x} &=& \dfrac{2(x^2-1)}{x} \\\\&=&\dfrac{2(x+1)(x-1)}{x} \end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} \forall x\in]0;+\infty[\text{ : } g'(x)&=&\left(x^2-2\ln x\right)'&=& 2x-2\times \dfrac{1}{x}\\\\ &=& \dfrac{2x^2-2}{x} &=& \dfrac{2(x^2-1)}{x} \\\\&=&\dfrac{2(x+1)(x-1)}{x} \end{matrix})
![\boxed{\forall x\in]0;+\infty[\text{ : }g'(x)=\dfrac{2(x+1)(x-1)}{x}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in]0;+\infty[\text{ : }g'(x)=\dfrac{2(x+1)(x-1)}{x}})
b) On sait que pour tout réel
strictement positif: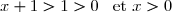 
.
Donc le signe de)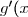
est celui de 
, dressons le tableau de signe de 
Alors:
![\boxed{\begin{matrix} \bullet & \forall x\in ]0;1[\text{ : }g'(x)<0 \\ \bullet & g'(1)=0 \\ \bullet & \forall x\in ]1;+\infty[\text{ : }g'(x)>0 \end{matrix}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\begin{matrix} \bullet & \forall x\in ]0;1[\text{ : }g'(x)<0 \\ \bullet & g'(1)=0 \\ \bullet & \forall x\in ]1;+\infty[\text{ : }g'(x)>0 \end{matrix}} )
c) On tire de ce qui précède directement que:
![\boxed{\begin{matrix} \bullet & g\text{ est strictement décroissante sur } ]0;1[\\ \bullet & g\text{ admet un minimum en }1 \\ \bullet & g\text{ est strictement croissante sur } ]1;+\infty[\end{matrix}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\begin{matrix} \bullet & g\text{ est strictement décroissante sur } ]0;1[\\ \bullet & g\text{ admet un minimum en }1 \\ \bullet & g\text{ est strictement croissante sur } ]1;+\infty[\end{matrix}} )
Or,=1^2-2\ln 1=1)
, et on dresse le tableau de variations de la fonction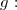 
 & \dbarre & - &\barre{0} & + & \\ \hline & +\infty & & & &+\infty \\ g & \dbarre &\searrow& & \nearrow & \\ & \dbarre & & g(1)=1 & & \\ \hline \end{array}} )
3) La fonction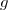 amdet un minimum en 
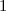, alors, pour tout ![x\in ]0;+\infty[\text{ : }g(x)\geq g(1)=1 >0](https://latex.ilemaths.net/latex-0.tex?x\in ]0;+\infty[\text{ : }g(x)\geq g(1)=1 >0)
Donc:
![\boxed{ \forall x\in]0;+\infty[\text{ : }g(x) >0}](https://latex.ilemaths.net/latex-0.tex?\boxed{ \forall x\in]0;+\infty[\text{ : }g(x) >0})
Partie B:
![\forall x\in]0;+\infty[\text{ : }f(x)=\dfrac{x}{2}+\dfrac{1+\ln x}{x}](https://latex.ilemaths.net/latex-0.tex?\forall x\in]0;+\infty[\text{ : }f(x)=\dfrac{x}{2}+\dfrac{1+\ln x}{x})
1)
La limite en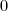 à droite:
 &=& \displaystyle\lim_{x\to 0^+}\dfrac{x}{2}+\dfrac{1+\ln x}{x} &=& 0+\dfrac{1+(-\infty)}{0^+} &=& (-\infty)\times (+\infty) &=& -\infty\end{matrix} )
La limite en :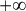
 &=& \displaystyle\lim_{x\to +\infty}\dfrac{x}{2}+\dfrac{1+\ln x}{x} &=& \displaystyle\lim_{x\to +\infty}\dfrac{x}{2}+\dfrac{1}{x}+\dfrac{\ln x}{x}&=& (+\infty)+0+0 &=& +\infty \end{matrix} )
Conclusion:
=-\infty\enskip\text{ et }\enskip \displaystyle\lim_{x\to +\infty}f(x)=+\infty})
Puisque=-\infty)
, donc:
 }\text{est une asymptote verticale à }(C)\text{ dirigée vers le bas}})
2-a) La fonction
est dérivable sur comme somme de fonctions dérivables sur cet intervalle.
![\begin{matrix} \forall x\in]0;+\infty[\text{ : } f'(x)&=&\left(\dfrac{x}{2}+\dfrac{1+\ln x}{x}\right)'&=& \dfrac{1}{2}+ \dfrac{(1+\ln x)'x-(1+\ln x)}{x^2}\\\\ &=& \dfrac{1}{2}+\dfrac{\dfrac{1}{x}\times x -1-\ln x}{x^2} &=& \dfrac{1}{2}- \dfrac{\ln x}{x^2} \end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} \forall x\in]0;+\infty[\text{ : } f'(x)&=&\left(\dfrac{x}{2}+\dfrac{1+\ln x}{x}\right)'&=& \dfrac{1}{2}+ \dfrac{(1+\ln x)'x-(1+\ln x)}{x^2}\\\\ &=& \dfrac{1}{2}+\dfrac{\dfrac{1}{x}\times x -1-\ln x}{x^2} &=& \dfrac{1}{2}- \dfrac{\ln x}{x^2} \end{matrix})
![\boxed{\forall x\in]0;+\infty[\text{ : }f'(x)=\dfrac{1}{2}- \dfrac{\ln x}{x^2}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in]0;+\infty[\text{ : }f'(x)=\dfrac{1}{2}- \dfrac{\ln x}{x^2}})
Et en Mettant les deux fractions au même dénominateur, on obtient:
![\forall x\in]0;+\infty[\text{ : }f'(x)=\dfrac{1}{2}- \dfrac{\ln x}{x^2}=\dfrac{x^2-2\ln x}{2x^2} \Longrightarrow \boxed{ \forall x\in ]0;+\infty[\text{ : }f'(x)=\dfrac{g(x)}{2x^2} }](https://latex.ilemaths.net/latex-0.tex?\forall x\in]0;+\infty[\text{ : }f'(x)=\dfrac{1}{2}- \dfrac{\ln x}{x^2}=\dfrac{x^2-2\ln x}{2x^2} \Longrightarrow \boxed{ \forall x\in ]0;+\infty[\text{ : }f'(x)=\dfrac{g(x)}{2x^2} })
b) Puisque pour tout réel strictement positif,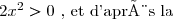 
Partie A >0)
.
On en déduit que:>0 })
On en tire que:
![\boxed{\text{ La fonction }f\text{ est strictement croissante sur }]0;+\infty[}](https://latex.ilemaths.net/latex-0.tex?\boxed{\text{ La fonction }f\text{ est strictement croissante sur }]0;+\infty[})
Dressons le tableau de variations de la fonction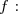
 & \dbarre & + & \\ \hline & \dbarre & &+\infty \\ f & \dbarre & \nearrow & \\ & -\infty & & \\ \hline \end{array}} )
3-a) Calculons la limite-y\text{ : })
-y&=&\displaystyle\lim_{x\to +\infty}\dfrac{x}{2}+\dfrac{1+\ln x}{x}-\dfrac{x}{2} &=& \displaystyle\lim_{x\to +\infty}\dfrac{1}{x}+\dfrac{\ln x}{x}&=&0+0&=&0\end{matrix} )
Interprétation graphique:
\text{ d'équation }y=\dfrac{1}{2}x\text{ est une asymptote oblique à }(C)\text{ au voisinage de }+\infty})
Etude de la position relative de)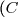
par rapport à \text{ : })
On a pour tout réel![x\in ]0;+\infty[\text{ : }f(x)-y=\dfrac{x}{2}+\dfrac{1+\ln x}{x}-\dfrac{x}{2}=\dfrac{1+\ln x}{x}](https://latex.ilemaths.net/latex-0.tex?x\in ]0;+\infty[\text{ : }f(x)-y=\dfrac{x}{2}+\dfrac{1+\ln x}{x}-\dfrac{x}{2}=\dfrac{1+\ln x}{x} )
De plus, pour tout réel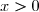
, le signe de -y)
est celui de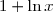 
, étudions alors ce signe.
Résolvons pour cela l'équation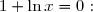
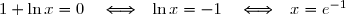
Par croissance de la fonction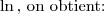
![\begin{matrix} \forall x\in ]0;e^{-1}[\text{ : }0>1+\ln x \\ \text{ Pour }x=e^{-1} \text{ : } 1+\ln x=0 \\ \forall x\in ]e^{-1};+\infty[\text{ : }1+\ln x>0\end{matrix} \enskip\enskip\text{ , donc : }\enskip\enskip \begin{matrix} \forall x\in ]0;e^{-1}[\text{ : }0> f(x)-y \\ \text{ Pour }x=e^{-1} \text{ : } f(x)-y=0 \\ \forall x\in ]e^{-1};+\infty[\text{ : }f(x)-y>0\end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} \forall x\in ]0;e^{-1}[\text{ : }0>1+\ln x \\ \text{ Pour }x=e^{-1} \text{ : } 1+\ln x=0 \\ \forall x\in ]e^{-1};+\infty[\text{ : }1+\ln x>0\end{matrix} \enskip\enskip\text{ , donc : }\enskip\enskip \begin{matrix} \forall x\in ]0;e^{-1}[\text{ : }0> f(x)-y \\ \text{ Pour }x=e^{-1} \text{ : } f(x)-y=0 \\ \forall x\in ]e^{-1};+\infty[\text{ : }f(x)-y>0\end{matrix} )
Finalement, on calcule=\dfrac{e^{-1}}{2}+\dfrac{1+\ln e^{-1}}{e^{-1}}=\dfrac{1}{2e}+\dfrac{1-1}{e^{-1}}=\dfrac{1}{2e})
On en déduit que:
![\boxed{\begin{cases} (C) \text{ est en dessous de }(D)\text{ sur }]0;e^{-1}[ \\ (C) \text{ coupe }(D) \text{ au point }K\left(\dfrac{1}{e};\dfrac{1}{2e}\right) \\ (C) \text{ est au-dessus de }(D)\text{ sur }]e^{-1};+\infty[\end{cases}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\begin{cases} (C) \text{ est en dessous de }(D)\text{ sur }]0;e^{-1}[ \\ (C) \text{ coupe }(D) \text{ au point }K\left(\dfrac{1}{e};\dfrac{1}{2e}\right) \\ (C) \text{ est au-dessus de }(D)\text{ sur }]e^{-1};+\infty[\end{cases}} )
b) Le coefficient directeur de)
étant 
, l'abscisse du point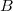 
qu'on note 
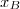doit vérifier =\dfrac{1}{2} )
.
=\dfrac{1}{2}&\iff& \dfrac{g(x_B)}{2x_B^2}=\dfrac{1}{2} &\iff& g(x_B)=x_B^2 \\&\iff& x_B^2-2\ln x_B=x_B^2 &\iff& \ln x_B=0\\ &\iff& x_B=1 \end{matrix})
Et on calcule l'ordonnée de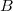 qu'on note \text{ : })
=\dfrac{x_B}{2}+\dfrac{1+\ln x_B}{x_B}=\dfrac{1}{2}+\dfrac{1+\ln 1}{1}=\dfrac{1}{2}+1=\dfrac{3}{2} )
 })
4) D'après la question précédente, le point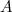
n'est autre que le point 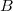, et on a déjà calculé : =\dfrac{1}{2} \text{ et }f(1)=\dfrac{3}{2})
Donc la tangente)
au point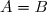 
a pour équation :
\text{ : }y=f'(1)(x-1)+f(1) \iff (T)\text{ : }y=\dfrac{1}{2} (x-1)+\dfrac{3}{2} \iff \boxed{(T)\text{ : }y=\dfrac{1}{2}x+1 })
5) Le graphique:
Bac Mathématiques
Burkina Faso 2023
Série A4
1er tour
Coefficient: 3
Calculatrice non autorisée
5 points
exercice 1
6 points
exercice 2
9 points
probleme
exercice 1
1) On a
Puisque
2-a) On a trouvé que
Donc, directement:
b) Puisque
Donc:
c) Résolvons l'équation
3-a) Résolvons l'équation
b) Résolvons l'équation
exercice 2
On note
1-a) Directement d'après l'énoncé:
Si le joueur obtient
Si le joueur obtient
Si le joueur obtient
b) Dressons un arbre pondéré:
On a donc:
Et on représente la loi de probabilité de
c) Calculons l'espérance mathématique
d) L'espérance mathématique est négative, donc:
2-a) Directement d'après l'énoncé:
Si le joueur obtient
Si le joueur obtient
Si le joueur obtient
b) De la même manière, et en utilisant le même arbre pondéré, on trouve:
Et on représente la loi de probabilité de
c) Calculons l'espérance mathématique
3) Le jeu est équitable si et seulement si l'espérance mathématique est nulle, donc:
probleme
Partie A:
1)
La limite en
La limite en
Conclusion:
2-a) La fonction
b) On sait que pour tout réel
Donc le signe de
Alors:
c) On tire de ce qui précède directement que:
Or,
3) La fonction
Donc:
Partie B:
1)
La limite en
La limite en
Conclusion:
Puisque
2-a) La fonction
Et en Mettant les deux fractions au même dénominateur, on obtient:
b) Puisque pour tout réel
On en déduit que:
On en tire que:
Dressons le tableau de variations de la fonction
3-a) Calculons la limite
Interprétation graphique:
Etude de la position relative de
On a pour tout réel
De plus, pour tout réel
Résolvons pour cela l'équation
Par croissance de la fonction
Finalement, on calcule
On en déduit que:
b) Le coefficient directeur de
Et on calcule l'ordonnée de
4) D'après la question précédente, le point
Donc la tangente
5) Le graphique:
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Voir la correction
forum de terminale