Remarque : Fiche à travailler en ligne, seule la page 1 est téléchargeable.
I. Définitions
Soit
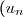_{n \in \textbf{N}})
une suite à valeurs dans
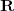
ou

. On lui associe une nouvelle suite
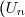_{n\ \in \textbf{N}})
en posant
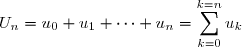
Le couple
 \, , \, (U_n)\right))
est appelé la
série de terme général 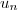
. On notera

la série
 \, , \, (U_n)\right))
.
Le nombre
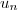
est le
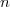 -ième terme
-ième terme et le nombre
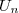
est la
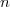 -ième somme partielle
-ième somme partielle de la série

.
On convient que si la suite
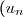)
est définie seulement pour
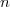
supérieur à un entier
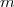
, on pose

, de sorte que
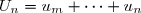
pour
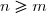
.
L'étude de la
série 
est l'étude de la
suite 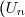_{n \in \textbf{N}})
. On dira donc que la série

est
convergente si et seulement si la suite
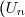)
est convergente et on dira que la série

est
divergente si et seulement si la suite
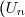)
est divergente.
Si la série

est convergente, on appelle
somme de cette série le nombre
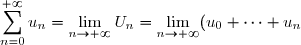)
et, pour chaque entier
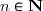
, on appelle
reste de rang 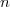
de la série le nombre
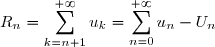
Il arrive que pour une série convergente, on note
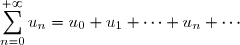
On dit qu'une série

est
absolument convergente si et seulement si la série
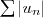
est convergente. Une série qui est convergente, mais qui n'est pas absolument convergente, est une série
semi-convergente.
Une série

est à
termes positifs si et seulement si
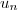
est un nombre réel positif pour tout
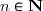
. Une série
alternée est une série

dont tous les termes sont réels et telle que
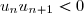
pour tout
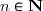
.
Soient

et

deux séries. On appelle
produit de Cauchy de ces séries et on note

la série
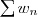
où
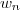
est défini pour chaque
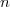
par
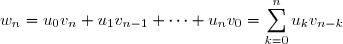
II. Propriétés générales
On ne change pas la nature d'une série si on modifie un nombre
fini de ses termes. Si elle était divergente, elle reste divergente ; si elle était convergente, elle reste convergente, mais sa somme peut changer.
Si

et

sont des séries convergentes et si
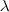
et
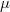
sont des nombres complexes, alors la série
)
est convergente et on a
 = \lambda \displaystyle \sum_{n=0}^{+\infty} u_n + \mu \displaystyle \sum_{n=0}^{+\infty} v_n)
Soient
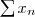
et
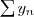
des séries réelles. La série complexe
)
est convergente si et seulement si les séries
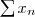
et
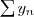
sont convergentes.
Si

est une série convergente, alors
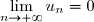
.
Critère de Cauchy :
Une série

est convergente si et seulement si
 \, \left(\exists n_0 \in \textbf{N}\right) \, \left(\forall p \in \textbf{N}\right) \, \left(\forall q \in \textbf{N}\right) \, \left(p > q \geq n_0 \Rightarrow \left|u_{q+1} + u_{q+2} + \cdots + u_p \right| \leq \varepsilon\right))
A une série

on associe une nouvelle série

obtenue en calculant d'abord des sommes de termes consécutifs de la série donnée. Précisément, on se donne une application strictement croissante
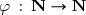
et on pose
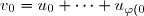} \hspace{15pt} \text{et} \hspace{15pt} v_n = u_{\varphi(n-1)+1} + \cdots + u_{\varphi(n)} \text{ pour } n \geq 1)
de sorte que les sommes partielles
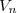
de

vérifient
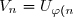})
.
Avec ces notations, si la série

converge, alors la série

converge aussi et
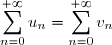
. La réciproque est fausse mais on a la proposition suivante :
Si

converge et si
 + 1}\| + \cdots + \|u_{\varphi(n)}\|) = 0)
alors

converge et
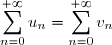
.
En particulier, si
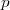
est un entier supérieur à 2 et si les termes sont groupés
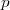
par
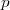
, c'est-à-dire si
 = p(n+1)-1)
, on peut affirmer que si

converge et si
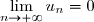
, alors

converge et
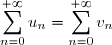
.
III. Séries à termes positifs
Dans tout ce paragraphe, toutes les séries ont tous leurs termes réels positifs. Si

est une telle série, la suite
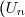)
de ses sommes partielles est une suite à termes réels positifs qui est croissante. On sait qu'il y a exactement deux possibilités :
la suite
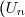)
n'est pas bornée, et alors
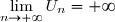
et la série

est divergente.
la suite
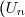)
est bornée, et alors elle admet pour limite sa borne supérieure ; dans ce cas la série

est convergente et
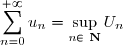
.
Principe de comparaison :
Soient

et

deux séries telles que
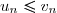
pour tout
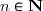
. Alors :
si

diverge,

diverge.
si

converge,

converge et
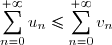
.
Proposition :
Soient

et

deux séries à termes positifs. On suppose que
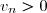
pour
tout
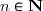
. Alors
si

converge et si
 = 0)
, alors

converge.
si

diverge et si
 = +\infty)
, alors

diverge.
si la suite
)
a une limite non nulle, alors les deux séries

et

sont de même nature.
Règle de d'Alembert :
Soit

une série à termes strictement positifs telle que la suite
)
admette une limite

.
Si
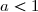
, la série converge et si
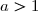
, la série diverge.
Règle de Cauchy :
Soit

une série à termes strictement positifs telle que la suite
![\sqrt[n]{u_n}](https://latex.ilemaths.net/latex-0.tex?\sqrt[n]{u_n})
admette une limite

.
Si
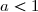
, la série converge et si
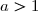
, la série diverge.
Règle
n un
un :
Soient

une série à termes positifs et

un nombre réel.
si
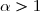
et si la suite
)
a une limite, alors la série

converge.
si
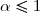
et si la suite
)
a une limite non nulle ou tend vers
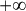
, alors la série

diverge.
Comparaison avec une intégrale :
Soit
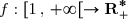
une fonction décroissante.
La série
)
est convergente si et seulement si l'intégrale
 \, dt)
est convergente et, lorsque c'est le cas, on a
 \leq \displaystyle \int_ 1^{+\infty}f(t) \, dt \leq \sum_{n=1}^{+\infty} f(n))
Sommation par tranches :
Soient

une série à termes positifs,
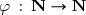
une fonction strictement croissante et

la série associée en sommant par tranches.
Les séries

et

sont de même nature et, si elles convergent, on a
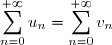
Dans la mesure ou on peut changer un nombre fini de termes d'une série sans modifier sa nature, les résultats de ce paragraphe, dès lors qu'ils ne concernent que la nature des séries, peuvent s'appliquer si les hypothèses sont vérifiées sauf pour un nombre fini de termes.
IV. Séries absolument convergentes
Si une série

, réelle ou complexe, est absolument convergente, alors elle est convergente et on a
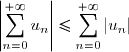
Convergence commutative :
Soient

, une série absolument convergente et
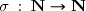
une bijection.
La série
})
est absolument convergente et l'on a
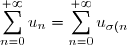})
.
Théorème de Cauchy-Mertens :
Soient

, une série absolument convergente et

une série convergente.
Leur produit de Cauchy
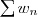
est une série convergente et
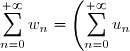 \left(\displaystyle \sum_{n=0}^{+\infty} v_n \right))
. Si

est elle aussi absolument convergente, alors
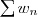
est absolument convergente.
V. Séries semi-convergentes
Théorème de Leibniz pour les séries alternées :
Soit
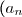)
une suite positive décroissante qui tend vers 0.
La série alternée
^n a_n)
est convergente et, en notant
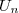
ses sommes partielles, on a pour tout
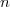
^n a_n \leq U_{2n})
Soit

, une série dont le terme général est écrit sur la forme
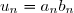
. On note
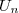
et
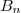
les sommes partielles des séries

et
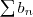
. On a
 + \cdots + a_n(B_n - B_{n-1}) \\ & = (a_0-a_1)B_0 + (a_1-a_2)B_1 + \cdots +(a_{n-1}-a_n)B_{n-1} + a_nB_n\\ & = \displaystyle \sum_{k=0}^{n-1} (a_k - a_{k+1})B_k + a_nB_n \end{array})
Le procédé qui nous fournit cette expression de
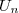
est appelé la
transformation d'Abel. On voit donc que si la série
B_n)
et la suite
)
sont convergentes, alors la série

converge. Un cas ou ces conditions sont vérifiées est fourni par le
Théorème d'Abel :
Soient
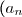)
une suite réelle décroissante et
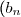)
une suite complexe.
Si la suite
)
des valeurs absolues des sommes partielles de la série
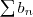
est majorée et si
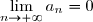
, alors la série
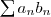
est convergente.
VI. Exemples et contrexemples
Séries géométriques :
Pour
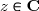
, on appelle
série géométrique de raison 
la série
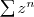
.
si
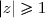
, la série
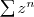
diverge.
si
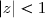
, la série
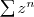
converge et
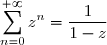
.
Soit
.
Une série de Riemann est une série de la forme
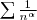
(bien entendu, définie pour
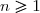
).
La série
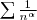
converge si et seulement si
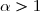
.
Pour
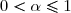
, la série
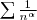
est donc divergente bien que son terme général tende vers 0.
La série
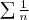
est appelée la série
harmonique.
Par ailleurs, si on note
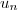
le terme général d'une série de Riemann, on voit que dans tous les cas
 = 1)
et que
![\displaystyle \lim_{n \to +\infty} \sqrt[n]{u_n} = 1](https://latex.ilemaths.net/latex-0.tex?\displaystyle \lim_{n \to +\infty} \sqrt[n]{u_n} = 1)
ce qui montre que si le nombre

qui figure dans les règles de d'Alembert et de Cauchy vaut 1, ces règles ne permettent pas d'en déterminer la nature.
Développement décimal :
Considérons une série de la forme
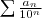
, où
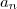
est un entier tel que
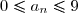
et
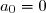
. Une telle série est convergente, et on a
![\displaystyle \sum_{n=0}^{+\infty} \frac{a_n}{10^n} \in [0 \, , \, 1]](https://latex.ilemaths.net/latex-0.tex?\displaystyle \sum_{n=0}^{+\infty} \frac{a_n}{10^n} \in [0 \, , \, 1])
. On prouve que tout réel
![x \in [0 \, , \, 1]](https://latex.ilemaths.net/latex-0.tex?x \in [0 \, , \, 1])
est somme d'une telle série, que l'on appelle un
développement décimal de 
. S'il existe un entier
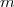
tel que
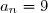
pour
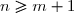
, on dit que le développement est
impropre. Considérons un réel
![x \in [0 \, , \, 1]](https://latex.ilemaths.net/latex-0.tex?x \in [0 \, , \, 1])
qui admet un développement impropre
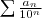
et soit
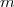
tel que
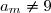
et
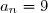
pour
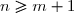
. Puisque
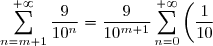^n = \frac{9}{10^{m+1}} \: \frac{1}{1-1/10} = \frac{1}{10^m})
on a aussi
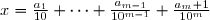
et

admet un deuxième développement décimal propre (et fini).
Série exponentielle :
Il s'agit de la série
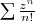
pour
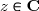
. Cette série est absolument convergente pour chaque

; on pose
 = \displaystyle \sum_{n=0}^{+\infty} \frac{z^n}{n!})
et la fonction ainsi définie est appelée l'
exponentielle complexe. On démontre que
 = e)
, où

est la base du logarithme népérien et que pour
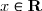
on a
 = e^x)
. Ceci justifie l'écriture
 = e^z)
pour tout
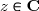
. Si
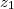
et
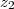
sont des nombres complexes, en calculant le produit de Cauchy
 \star \left(\sum \frac{z_2^n}{n!}\right))
on voit que
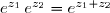
. En particulier, il en résulte que
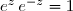
et par suite que
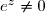
pour tout
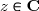
.
Les fonctions trigonométriques, sinus
)
et cosinus
)
et les fonctions sinus hyperbolique
)
et cosinus hyperbolique
)
sont définies sur

à partir de l'exponentielle par
 = \displaystyle \sum_{n=0}^{+\infty} (-1)^n \frac{z^{2n+1}}{(2n+1)!} = \frac{e^{iz}-e^{-iz}}{2i} & \hspace{15pt} & sh(z) = \displaystyle \sum_{n=0}^{+\infty} \frac{z^{2n+1}}{(2n+1)!} = \frac{e^z-e^{-z}}{2} \\ \cos(z) = \displaystyle \sum_{n=0}^{+\infty} (-1)^n \frac{z^{2n}}{(2n)!} = \frac{e^{iz}+e^{-iz}}{2} & & ch(z) = \displaystyle \sum_{n=0}^{+\infty} \frac{z^{2n}}{(2n)!} = \frac{e^z+e^{-z}}{2} \end{array})
Si
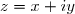
avec

et
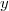
réels, on a
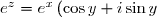)
et
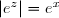
.
Remarques sur les règles de d'Alembert et Cauchy :
Soit

une série à termes strictement positifs. On démontre que si la suite
)
tend vers

, il en est de même pour la suite
![(\sqrt[n]{u_n})](https://latex.ilemaths.net/latex-0.tex?(\sqrt[n]{u_n}))
. Si, en ayant appliqué la règle de d'Alembert, on se trouve dans le cas
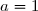
qui ne permet pas de conclure, il est inutile d'essayer la règle de Cauchy. En revanche, si la suite
)
n'a pas de limite, la règle de Cauchy peut permettre de conclure.
Par exemple, pour la série

définie par
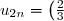^n)
et
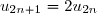
, la suite
)
n'a pas de limite, mais
![\displaystyle \lim_{n \to +\infty} \sqrt[n]{u_n} = \sqrt{\frac{2}{3}} < 1](https://latex.ilemaths.net/latex-0.tex?\displaystyle \lim_{n \to +\infty} \sqrt[n]{u_n} = \sqrt{\frac{2}{3}} < 1)
ce qui montre que cette série converge.
Par ailleurs, dans la mesure où ces deux règles consistent à comparer la série proposée à une série géométrique, on peut en cas de besoin alléger un peu les hypothèses. Par exemple, même si la suite
)
n'a pas de limite, mais vérifie
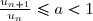
pour
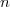
supérieur à un
entier
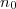
, on a
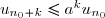
et le principe de comparaison montre que la série converge.
La série harmonique alternée :
Il s'agit de la série
^{n}}{n+1})
. C'est une
série alternée semi-convergente (exemple de série qui converge mais pas absolument). On a
^n}{n+1} = \ln 2)
Considérons la série

suivante :
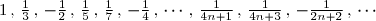
qui a les mêmes termes que la série harmonique alternée, mais dans un autre ordre. En groupant ces termes 3 par 3, on obtient une nouvelle série
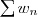
définie par
(4n+1)(4n+3)})
C'est une série à termes positifs et, puisque
)
tend vers
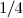
, elle converge, et
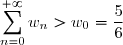
. Alors, par sommation par tranches, on voit que

converge et a la même somme que
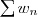
. On a donc
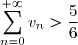
. Mais
^{n}}{n+1} < 1 - \frac{1}{2} + \frac{1}{3} = \frac{5}{6})
et par suite
^n}{n+1} \neq \displaystyle \sum_{n=0}^{+\infty} v_n)
. La série harmonique alternée n'est donc pas commutativement convergente.
Un produit de Cauchy de séries convergentes qui est divergent :
Considérons la série

où
^{n+1}}{\sqrt{n+1}})
. Il s'agit d'une série alternée qui est convergente d'après le théorème de Leibniz, mais qui n'est pas absolument convergente, puisque
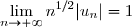
. Soit
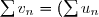 \star \left(\sum u_n \right))
. On a alors
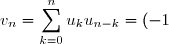^n \displaystyle \sum_{k=0}^n \frac{1}{\sqrt{k+1} \, \sqrt{n-k+1}})
Pour
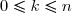
on a
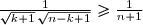
et par suite
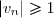
et, puisque
)
ne tend pas vers 0, la série

diverge.
Exemple de sommation par tranches d'une série divergente :
Soient
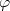
et
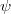
les applications
de
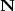
dans
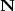
définies par
 = n(n+1))
et
 = (n+1)^2)
. Soit
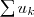
la série définie par
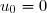
,
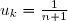
si
 < k \leq \psi(n))
et
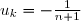
si
 < k \leq \varphi(n+1))
. Les premiers termes de cette série sont
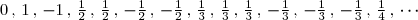
Si on note
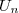
les sommes partielles de cette série, on voit que
} = 0)
et
} = 1)
pour tout
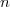
. Les sommations par tranches associées aux applications
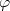
et
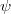
sont donc convergentes et donnent des sommes distinctes. La suite
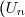)
admettant deux suites extraites de limites différentes, la série

est divergente.
VII. Plan d'étude d'une série
Pour finir, voici un plan et quelques conseils pour étudier une série

.
1. A-t-on
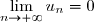
? Si non, la série est divergente. Si oui, elle garde toutes ses chances de
converger.
2. La série est-elle absolument convergente ? On est amené à étudier la série à termes positifs
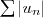
. En général les tests de d'Alembert, de Cauchy ou des comparaisons permettent de conclure. Si elle est absolument convergente, elle est convergente ; sinon, elle a encore une chance d'être semi-convergente (si elle n'est pas à termes positifs).
3. On essaie d'appliquer le théorème de Leibniz pour une série alternée, ou la transformation d'Abel si Leibniz ne convient pas.
Il se peut qu'aucune de ces méthodes ne permette de conclure. Il faut garder présent à l'esprit que, hormis le critère de Cauchy qui est très malaisé à appliquer, tous les résultats que nous avons mentionnés fournissent des conditions ou bien nécessaires, ou bien suffisantes de convergence, mais pas les deux. Il reste donc toujours quelques cas non couverts (et dans la littérature on trouve bien d'autres tests de convergence).
Il faut aussi comprendre qu'en général on ne sait pas calculer la somme d'une série convergente. L'intérêt des séries est justement le fait que les sommes partielles fournissent des approximations aussi bonnes que l'on désire de la somme que l'on ne connaît pas. L'exemple type est le nombre irrationnel 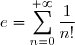 dont on peut calculer la valeur avec une bonne précision en calculant les sommes partielles. Ainsi, la 7-ème somme partielle vaut
dont on peut calculer la valeur avec une bonne précision en calculant les sommes partielles. Ainsi, la 7-ème somme partielle vaut 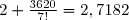 , et on voit que l'erreur est inférieure à 10-4, donc
, et on voit que l'erreur est inférieure à 10-4, donc 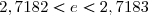 .
.
 un :
un : dont on peut calculer la valeur avec une bonne précision en calculant les sommes partielles. Ainsi, la 7-ème somme partielle vaut
, et on voit que l'erreur est inférieure à 10-4, donc
.

 analyse en post-bac
analyse en post-bac