Inscription / Connexion Nouveau Sujet
Base orthonormée, espace vectoriel
Bonjour,
Mon concours de pharmacie approche, je fais des annales et j'ai donc quelques questions auxquelles je ne sais pas trop répondre.
On dit que :
L'espace vectoriel euclidien orienté 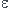 , de dimension 3, est rapporté à une base orthonormée (
, de dimension 3, est rapporté à une base orthonormée (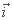
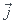
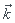 ) directe
) directe
1/ On me donne : (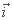 ,-
,-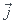 ,
,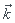 ),(-
),(-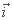 ,-
,-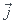 ,
,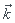 ) et (-
) et (-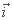 ,-
,-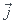 ,-
,-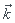 )
)
Je dois dire si ce sont des bases orthonormée directes ou indirectes.
Je dirais qu'elles sont indirectes mais j'hésite avec la dernière
2/ On pose 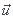 =(
=(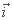 +
+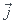 )
) (
(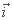 -
-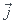 )
)
On me demande d'exprimer 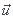 en fonction de
en fonction de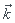
et 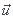 .
.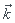
Je pense que ca ne doit pas être si compliqué, mais comme on ne fait pas d'exercice, il faut tout trouver par nous même.
Merci de m'aider

salut
si les 2 premières sont indirectes (et c'est le cas) alors la dernière est directe
enfin j'hésite pour la 2°
pour la question 2) distribue ton produit vectoriel par rapport à la somme (ou différence)

je ne comprends pas comment je peux distribuer le produit, il n'y a pas de valeurs. Je n'ai aucune notion sur ce cours, il faut tout m'expliquer 
Une petite erreur s'est glissée , c'est 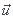 =(
=(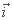 +
+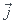 )
) (
(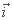 .
.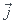 )
)
à mon avis il y a une erreur dans ton dernier post:
le produit vectoriel (^) s'applique à deux vecteurs et le prduit scalaire (.) donne un nombre...
Excuse moi, il n'y avait pas d'erreur dans le premier post, c'est bien un addition puis une soustraction
Bonsoir.
1°) La première et la troisième bases sont indirectes, la seconde est directe.
2°) u = (i+j)^(i-j) = i^i + j^i - i^j - j^j (par distributivité du produit vectoriel, c'est comme si tu avais (a+b)*(c+d))
i^i = j^j = 0, j^i = -i^j,
donc u = -2i^j, or i^j = k
donc finalement : u = -2k, et u.k = -2k.k = - 2 (car k est un vecteur unitaire)
Merci beaucoup, j'ai tout compris pour le 2, et ca coincide bien avec les réponse proposées (c'est un QCM).
Par contre, comment est-ce que l'on sait si les bases sont directes ou indirectes?
Ca dépend du ce que tu sais, mais le plus simple, je pense, c'est de se rappeler de la règle du triède (tu sais, celle ou on regarde avec les doigts de sa main  ), puis de faire un schèma avec i,j,k directe, tracer les bases proposées, et de regarder ta main
), puis de faire un schèma avec i,j,k directe, tracer les bases proposées, et de regarder ta main 
Y'en a que 2 qui sont directes alors (i,j,k) et (-i,-j,k) ?
Je fais la suite de l'exo et je bloque encore, on me demande de calculer
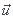 .
.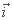 ,
, 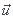 .
.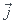 et
et 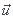 .
.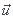
Oui, il n'y a que (i,j,k) et (-i,-j,k) (parmi celles proposées bien sur, il y en a bien d'autres)
Tu as maintenant l'expression de u, tu peux faire comme lorsque tu as calculé u.k 
Je trouve 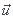 .
.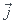 =-2
=-2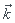 .
.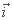 =-2
=-2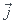 , mais les réponses proposées sont 0 et +1, peut être qu'aucune n'est la bonne)
, mais les réponses proposées sont 0 et +1, peut être qu'aucune n'est la bonne)
pour 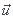 .
.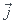 =-2
=-2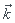 .
.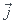 =2
=2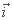 , c'est pareil, ils donnent comme choix 0 et +1.
, c'est pareil, ils donnent comme choix 0 et +1.
Ensuite, il y'a 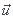 .
.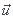 =4 , je pense que cette proposition est vraie
=4 , je pense que cette proposition est vraie
Bonjour
autre moyen de voir si les bases (orthonormées) sont directes ou non : si elles sont directes, le 1° vecteur vectoriel le 2° = le 3°, si elles sont indirectes, ça donne moins le 3°
Attention, un produit scalaire est un nombre !
car ces vecteurs sont orthogonaux
pareil pour k scalaire j
et u scalaire u = carré de la norme de u
donc pour 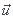 .
.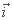 , je dois trouver 0 puisque
, je dois trouver 0 puisque 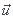 =-2
=-2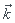 et
et 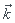 est perpendiculaire à
est perpendiculaire à 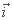 donc le produit scalaire est nul.
donc le produit scalaire est nul.
C'est bien ça?
En effet, c'est tout a fait ca.
Si deux vecteurs sont perpendiculaires, alors leur produit scalaire est nul.



 algèbre en post-bac
algèbre en post-bac