Inscription / Connexion Nouveau Sujet
d Ostrogradski
Bonjour tous le monde,
J'ai une question a laquelle je ne sais pas repondre :
Soit V(M) = yi - xj + zk
soit (A) le volume d'équation :
x² + y² < R²
y > R - x
0 < z < h
Dont la section z constant est représenté par l'intérieur de la courbe fermée (C)
1/ Ecrire la formule d'Ostrogradski liant le flux sortant du
champs de vecteur (V) à travers la surface bord de (A) et
une intégrale triple.
Préciser les équation de chacune des surfaces bord de (A)
Je ne connais pas cette formule ???
Bonjour!
Théorème de Green Ostrogradski
Soit S une surface fermée quelconque enfermant un volume V. Le flux sortant du champs de vecteurs 
à travers S est égale à l'integral triple de la divergence de A sur le volume
fermée .d
= sur le volume div d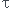
je ne sais pas si cela te sert à qqchose mais ce tout ce que j'ai
Bon courage
Bonjour!
Théorème de Green Ostrogradski
fermée 
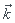.d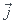
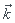= sur le volume div d
Annuler
connectez vous
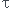
analyse en Bts