Enigmo 120 : Repas autour d'une table ronde

Posté par jamo jamo

Bonjour,

un peu de géométrie, de la vraie !

Quatre couples se retrouvent autour d'une table ronde pour un repas. Les quatre femmes s'installent en premier en se répartissant un peu n'importe comment autour de la table.
Ensuite, chacun des quatre hommes s'installe entre deux femmes. Mais, désireux de rétablir un peu d'ordre, chaque homme se place exactement à la même distance de ses deux voisines.

Marcel et René, les deux voisins de Paulette, sont situés à 1,35m l'un de l'autre.
Jean-Paul et Arnold, les deux voisins de Denise, sont situés à 1,82m l'un de l'autre.

Question : Quel est le rayon de la table ? (précision au millimètre)

Si jamais vous pensez qu'on ne peut pas résoudre le problème, alors répondez "problème impossible".

Bonne recherche !

Posté par plumemeteore plumemeteore

Bonjour Jamo.
La circonférence est le double de la somme des distances données.
Le rayon est la circonférence divisée par 2 pi, donc la somme divisée par pi : 1,009 m.

Ce serait un peu fort qu'il y ait des 'crabes' qui pensent que le problème est impossible

Posté par Nofutur2 Nofutur2

Je trouve un rayon de 1,133 m.

Posté par dpi dpi

La table est ronde et nous ne sommes pas en physique mais en géométrie donc homme et femmes seront considérés comme des points du cercle et non légèrement excentrés comme tout bon convive sur sa chaise. Nous obtenons un octogone non régulier  pour l'ensemble et deux quadrilatères pour les hommes et les femmes:
je trouve un diamètre de 1 120 ,7 mm

Posté par LeDino LeDino

Problème très amusant... En apparence insoluble, mais ayant pourtant bien une solution, et très simple qui plus est !

Le rayon de la table est de 1,133 mètres (1133 millimètres).

Explication :
Si on déplace une seule dame (les trois autres restant fixes), on s'aperçoit que ses deux voisins pivotent du même angle : ils restent donc toujours à même distance.

Mais alors on peut s'intéresser au cas particulier où les quatre dames sont assises en seulement deux points différents. Et dans ce cas, deux messieurs occupent les mêmes places qu'elles, tandis que les deux autres se trouvent sur un diamètre du cercle. Mais alors le triangle qui relie les messieurs est rectangle, et on peut déduire l'hypothénuse par Pythagore :

(2R)² = 1.35² + 1.82²
Et donc R = 1.133 m

Merci pour cette super énigme.

Posté par 13or 13or

Salut jamo!

Réponse : 1,133 m

Posté par castoriginal castoriginal

Bonsoir,

Suivant la figure ci-dessous, on considère les distances entre chaque convive L1,L2,L3,L4 puisque chaque homme se situe à égale distance de ses voisines.
En faisant abstraction des convives, on peut considérer que pour faire le tour de la table, on parcourt un quadrilatère de périmètre 2(1,35m + 1,82m). On peut intervertir le cheminement et l'on obtient un rectangle de côtés 1,35m x 1,82m
Le rayon d'un rectangle inscrit dans un cercle vaut R= (L²+h²⁾)^0,5  
                                                                                           2
soit  R=(1820²+1350²)^0,5/2

finalement R=1,133m   soit R=1133mm
                                                                                                                                                                            

                                    
                                                                                            

Posté par jeni231 jeni231

bonsoir,
R:rayon, D:diametre
R=D/2
*D=périmetre
périmetre=1.35*2+1.82*2=6.34

donc D=6.34/
et donc R=3.17/
merci.

Posté par yoyodada yoyodada

Bonsoir jamo

Merci pour cette énigme géométrique, ça change un peu

Pour la résolution j'ai utilisé le théorème d'Al-Kashi, et je trouve un rayon du cercle de R = 1133 millimètres[u][/u]  

Posté par geo3 geo3

Bonjour
Le rayon de la table = 113,3cm
A+

Posté par veleda veleda

bonsoir jamo,
je n'avais pas vu qu'il y avait de nouvelles énigmes.
si u,v,x,y sont les distances qui séparent Marcel,René,J-P et Arnold de leurs voisines féminines le périmètre  p de la table est égal à  2(u+v+x+y)
mais u+v=1,35m et x+y=1,82m=> p=2(1,35+1,82)m=2(3,17m)=2R si R est le rayon de la table donc
à 1mm prés par défaut

merci pour cet énigmo auquel j'espère avoir répondu correctement

Posté par MatheuxMatou MatheuxMatou

Bonsoir Jamo

Le rayon de la table vaut, à mon avis, en millimètres
C'est à dire environ 1133 millimètres

MM

Posté par Daniel62 Daniel62

Bonjour Jamo,

ma réponse: rayon de la table = 1,133 m

Posté par dhalte dhalte

Bonjour

Posté par Sairus008 Sairus008

G crois q le rayon est 1009 mm car 1.35+1.82 est la moitier du perimetre de la table

Posté par hypatie hypatie

Bonjour,

Je propose R = 1,009 m.

J'ai supposé que les distances données sont définies en faisant le tour de la table, et non à vol d'oiseau.

Si on appelle l₁ la distance qui sépare Marcel de ses voisines, l₂ la distance qui sépare René de ses voisines, l₃ la distance qui sépare Jean-Paul de ses voisines et l₄ la distance qui sépare Arnold de ses voisines, on a :
d(Marcel, René) = l₁ + l₂ = 1,35 m
d(Jean-Paul, Arnold) = l₃ + l₄ = 1,82 m

Or, le demi tour de table R = l₁ + l₂ + l₃ + l₄ = 3,17 m
d'où le résultat.

Merci une fois de plus pour cette énigme sympa.

Posté par bissextile bissextile

on appelle x la distance entre marcel et paulette, y la distance entre rené et paulette, z la distance entre jean-paul et denise et w la distance entre denise et arnold

on a donc x+y=135 (en cm)
et w+z= 182

On appelle P le périmètre du cercle

P= 2x + 2y+ 2w + 2z
(car il est égal à la distance entre marcel et paulette plus celle entre marcel et son autre voisine (qui est égal à la première) et cela pour tout les autres)

=>P= 2x + 2(135-x)+ 2w + 2(182-w)
<=>P=634 cm
Or dans un cercle on a P= 2*R*pi
donc R= P/2pi
      = 100.9 cm

Posté par Maher_91 Maher_91

bonjour,
Problème impossible ; Chaque homme(supposé un point) forme avec le voisin de sa voisine un triangle isocèle de sommet O centre de la table (supposé un cercle) avec Ô=. or on ne peut pas trouver deux triangles isocèles de sommet et de deux cotés d'extrémité O égaux(deux rayons) mais de base différente.(1.35 et 1.82).




Edit jamo : image placée sur le serveur de l'ile, merci d'en faire autant la prochaine fois.

Posté par Maher_91 Maher_91

grosse erreur   Ô= et non Ô=

Posté par frapedur57 frapedur57

bonjour,

je trouve un périmèter de 12,68m.
Donc nous avons une table ronde donc son périmètre vaut
2 x 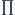x r = 12.68 m

Isolons 'r':

r =( 12.68 / 2 ) /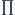
r = 6.34 /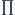
r = 2.018 m à 1mm près.

En espérant que ce soit la bonne réponse.

Posté par daxtero daxtero

1009 mm

Posté par lolo248 lolo248

Le rayon de la table est environ 1,145 m

Posté par LeDino LeDino

L'explication en image...

Les dames sont notées D1, D2, D3, D4.
Les messieurs sont notés H1, H2, H3, H4.

Posté par torio torio

1009 mm
= (1350+1820)*2/(2Pi)

J'ai considéré la distance "courbe" ( arc de cercle) qui
sépare deux personnes.

Posté par Rudi Rudi

Bonjour,

======== Réponse proposée ========

R = 1,133 m

Sauf erreur de raisonnement ou de calcul...

========= Méthode suivie ==========

Soit O le centre du cercle de rayon R recherché

Nommons les 4 points de l'énoncé par M pour Marcel, R pour René, P pour Paulette, J pour Jean-Paul, A pour Arnold et D pour Denise
Nommons les 4 angles a, b, c et d comme :
a = (OM, OP)
b = (OR, OP)
c = (OJ, OD)
d = (OA, OD)

On a alors 2(a+b+c+d) = 2pi soit (a+b)/2 = pi/2 - (c+d)/2

Exprimons la longueurs des cordes D=MR et L=AJ sous-tendues respectivement par les angles a+b et c+d :
D = 2Rsin((a+b)/2) d'où sin((a+b)/2) = D/2R
L = 2Rsin((c+d)/2) d'où sin((c+d)/2) = L/2R

de (a+b)/2 = pi/2 - (c+d)/2 on tire sin((a+b)/2) = sin(pi/2 - (c+d)/2) = cos((c+d)/2)

Elevons au carré :  sin²((a+b)/2) = cos²((c+d)/2) = 1 - sin²((c+d)/2) soit D²/4R² = 1 - L²/4R²

R = racine(D²+L²)/2 = 1,133 m

======== Remarque : valeurs entières de R ========

En prenant deux distances cathètes issues des triplets pythagoriciens non primitifs, par exemple D = 1,20 m et L = 1,60 m, on pouvait obtenir un rayon entier de valeur R = 1 m

======== Extension d'énoncé, poursuite de recherche =========

Avec les données de l'énoncé, déterminer la distance maximale entre deux femmes quelconques

( si je ne me suis pas trompé, cette distance ne peut excéder 1,083 m )

Rudy

Posté par gagou2713 gagou2713

Le rayon de la table est 1m45

Posté par jehanx jehanx

Semble impossible sans un élément supplémentaire : la distance entre
2 voisins (Paulette-Marcel par exemple).

Posté par cloraz01 cloraz01

le rayon est3.17/pi soit 1.009042

Posté par pacou pacou

Bonjour, Jamo

Je propose un rayon de 1009 mm au mm près pour une circonférence de 6,34 m.

Merci pour l'énigmo.

Posté par Kacs Kacs

Le rayon de la table est d'exactement , soit environ 1133 mm.

Posté par Tyvan Tyvan

1009 mm, si "sont situés à 1,35m" signifie que les deux personnes délimitent un arc de cercle de 1,35m avec la table.

Si "sont situés à 1,35m" signifie que la distance (au sens cartésien sqrt((x_a-x_b)²+(y_a-y_b)²)) entre les deux est de 1,35m, alors je trouve un rayon de 1133 mm, mais ma méthode est incomplète et je ne suis pas sûr qu'il n'existe qu'une seule solution.

Si quelqu'un a une idée de calcul dans le cas des distances cartésiennes, elle est la bien venue.

A plus

Posté par XJerem XJerem

la réponse est:

rayon = 2019mm

Posté par 1emeu 1emeu

Bonsoir,

ma réponse est "problème impossible" :
les distances entre Marcel et René et entre Jean-Paul et Arnold doivent être les mêmes

Merci pour l'énigme,

1emeu

Posté par kiko21 kiko21

Bonjour,

le rayon de la table est de

Pour la résolution, il suffit d'imaginer un gâteau avec 8 parts identiques deux à deux. On regroupe 4 parts différentes pour avoir la moitié du gâteau ce qui fait apparaitre un triangle rectangle de côtés 1,35m et 1,82m. On calcule alors l'hypoténuse qui correspond au diamètre.

Merci et A+, KiKo21.

Posté par chouchoupu chouchoupu

Le périmètre d'un cercle = 2*pi*rayon.
donc le rayon = périmètre/(2*pi)

Or le périmètre de la table ronde est :

1.35+1.82+1.35+1.82=6.34cm

rayon = 6.34/2*pi=2.17/pi= 0.69 cm = 6.9 mm

Posté par integral integral

Bonjour, le rayon de la table est 1,133 m au mm près
(c'est à dire ).
Merci pour cette énigme

Posté par manpower manpower

Bonsoir,

^{en considérant que la plus courte distance est la ligne droite (ici une corde), sinon le problème est trivial...}

je trouve (sauf erreur) une solution unique avec un rayon d'environ 91,4 cm.

Merci jamo pour l'Enigmo.

_{PS: En fan inconditionnel d'Asterix, j'approuve totalement le choix de l'image.}

Posté par godefroy_lehardi godefroy_lehardi

Bonjour,

Ma réponse est 1,009 m

Posté par evariste evariste

le rayon est de 1,133 m

Posté par gloubi gloubi

Bonjour,

La table a pour rayon 1133 mm.

Merci pour l'Enigmo !  

Posté par toddsalim toddsalim

Il s'agit de trouver les zéros de la focntion F définie par :
qui n'admet pas de zéro dans \{0} mais seulement si x+

donc je dirai problème impossible à résoudre

Posté par toddsalim toddsalim

je dirai problème impossible à résoudre si on cherche une valeur exacte mais si on veut approcher la valeur du zéro de la fonction F en utilisant par exemple Maple on trouvera que la solution est: 1.13301588691 cm

Posté par totti1000 totti1000

Salut Jamo je propose 1133mm...

Posté par jamo jamo

Clôture de l'énigme

La bonne réponse pour le rayon de la table est : 1133 mm

Beaucoup d'erreurs pour cette énigme !

Tout d'abord, il est dommage de confondre rayon et diamètre pour ceux qui ont utilisé une bonne méthode de résolution.

Ensuite, et j'ai été très étonné, beaucoup d'entre vous ont considéré que quand on parle de distance entre deux points situés sur un cercle, cette distance se mesure sur le cercle et non pas en ligne droite !!
A mon avis, ceux quoi ont fait ça l'ont fait dans le but de simplifier le problème.
J'attends de pied ferme les plaintes, mais je ne vois pas comment vous pourrez justifier ce choix (si j'avais pris une table carrée ou triangulaire, jamais vous n'auriez considéré que la distance se mesurait sur le bord de la table).

J'ai l'impression que certains ont utilisé des méthodes très compliquées pour arriver au résultat. Je livre donc une petite solution qui permettait de justifier que les deux distances que je donnais correspondaient aux côtés d'un triangle rectangle dont l'hypoténuse est le diamètre de la table, et cela sans passer par des fonctions compliquées et des calculs de trigo difficiles.

Sur la figure ci-dessous, j'ai noté G1, G2, G3, G4, F1, F2, F3 et F4 les filles et garçons. Pour respecter l'énoncé, deux angles de même couleur ont la même mesure.
Ainsi, on voit aisément que la somme des angles vus par les deux segments en rouge est égale à 180°.
Et donc, si on fait tourner le segment [G2G3] afin d'amener G2 sur G1, on obtient un triangle rectangle dont l'hypoténuse est égale au diamètre de la table.
Un petit coup de Pythagore, une division par 2, et c'est fini !

Posté par manpower manpower

Bonsoir,

En fan inconditionnel d'Asterix, merci Ordralphabetix pour ton poisson pas frais (mais mérité)!

Bon, j'ai traité tout en vrac à mon retour de vacances et hop ça commence les boulettes... je ne sais pas bien comment j'ai pu trouvé mon résultat (faux), mais je suis bien d'accord avec les 1133 mm.

Posté par kiko21 kiko21

Salut,



Erreur de débutant !!
Bornéo qui va me chambrer...

Merci Jamo et A+, KiKo21.