Problème sur la loi normale (TELUQ MQT-1001)

Posté par Lady001 Lady001

Bonjour.

Je remarque sur le forum que plusieurs personnes ont eu comme moi de la difficulté à résoudre le problème ci-dessous.  J'inscrit mon résultat sous le problème; quelqu'un pourrait-il me dire si mes déductions sont bonnes?  

Grand merci....

PROBLÈME:

Dans un examen imposé par la corporation des comptables à un très grand nombre de personnes, on considère que la note obtenue est une variable aléatoire normalement distribuée.  La note moyenne est de 70 et l'écart type est de 10.  La corporation des comptables décide que seulement 25% des participants seront accrédités par cet examen.  Quelle note faut-il obtenir pour être accrédité? Détaillez les étapes de vos calculs.

Note: Ce que vous devez rechercher ici est la valeur de x (la note) dans la formule z = (x - moyenne)/écart type.  IL vous faudra donc, après avoir identifié la cote z centrée réduite, isoler x dans cette formule.

MA SOLUTION:

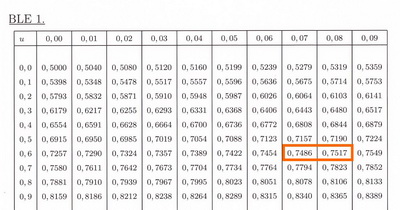
Pour 0,25 dans la table de la loi normale, on retrouve z=0,67 ou 0,68.

Soit: 0,67 = (x - 70)/10
6,7 = x - 70
76,7 = x

La note de passage pour être accrédité serait donc de 76,7.

Ai-je bon??

Merci à tous...ce travail est dû pour lundi le 22 mars, dans 3 jours...A l'aide!   

édit Océane : forum modifié

Posté par Lady001 Lady001

J'ai trouvé ma réponse dans un autre Post. Merci!!

Posté par Marguerite123 Marguerite123

Bonjour,

J'ai ce même problème à résoudre.  Est-ce que quelqu'un peut m'aider... En fait je ne comprends pas d'òu vient "Pour 0,25 dans la table de la loi normale, on retrouve z=0,67 ou 0,68"  Dans la table sous,25 j'ai 0,987.???

Merci à l'avance

Posté par Hiphigenie Hiphigenie

Bonjour,

Tu dois chercher dans la table la valeur de z pour laquelle 75% de la population se trouve en-dessous...

Regarde ce tableau.

Cela correspond à z = 0,675.