Inscription / Connexion Nouveau Sujet
Un rapport de distance minimale.
bonjour voilà, j'ai u devoir maison pour la semaine prochaine mais je ne m'en sors pas 
, pourriez-vous m'aider ?
ABC est une triangle tel que (vect AB;[vect AC)=2/3
, AB=3 et AC=5. La bissectrice intérieure de l'angle BAC coupe (BC) en A'. On désigne par d la demi-droite d'origine A passant par A'.
Pour M point quelconque de d, on pose : AM=x.
1.Montrer que, pour tout M de d on a : MB²=x²-3x+9 et MC²= x²-5x+25
2.f est la fonction définnie, pour tout réel x
0, par : f(x)=(x²-3x+9)/(x²-5x+25)
On note C sa courbe représentative dans le plan muni d'une repère orthogonal (0;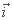
;
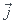)( unitées graphiques 0.5 sur l'axe des abscisses et 10 cm sur l'axe des ordonnées).
a) Etudier la limite de f en +
. interpréter graphiquement le résultat obtenu.
b) Déterminer la fonction dérivée de F sur [0;+[ et montrer que F' est du signe de p où p est la fonction définie par p(x)=-x²+16x-15 , pour tout x0.
c) Etudier les variations de F sur [0;+[ et dresser son tableau de variation.
3. a) En déduire que MB/MC est minimal en un point M1, de d et maximal en un point M2 de d.
b) vérifier que l'on a : M1B=
7 , M1C =21 , M2B= 321, M2C=57.
4. Démontrer que BC =7.
5.On note 
une mesure de l'angle en C du triangle M1BC et 
une mesure de l'angle en C du triangle M1AC.
a)Démontrer que cos=9/221.
b) calculer cos.
c) en déduire que M1 appartient à la bissectrice issue de C du triangle ABC et que M1 est le cente du cercle inscrit dans ce triangle.
6. a) Démontrer que le triangle M1BM2 est rectangle.
b) Quelle est la nature du triangle M1CM2 ?
c) sur quelles droites remarquables se situe M2?
7. Tracer la courbe représentative de F dans le repère (0;;).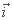
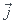8. a)Démontrer que l'équation f(x)=1 admet une unique solution x0dans [0;+[.
b) justifier géométriquement ce résultat.
c) Résoudre cette équation et montrer que le point M0 de d tel que AM0 =x0 est le centre d'un cercle passant par B,C,M1 et M2.
Merci d'avance pour vos réponses !
je n'arrive pas à retrouver la forme demandée avec la relation d'al-kashi :
1.MB²=MA²+AB²-2 MB MA cos(MAB) = x²+9-2x MB cos(MAB)
MC²= MA²+AC²-2 MA MC cos(MAC) = x²+25 - 2xMC cos(MAC).
2.a j'ai trouvé : lim f(x)=1 en +
b.f'(x)= (-x²+16x-15)/2(x²-5x+25)² . Comme 2(x²-5x+25)² est positif, f'(x) est du signe de p(x).
c.p(x)>0 pour x
[1;15]
3.a) MB/MC minimal pour M1=1
Mb/MC maximale pour M2=15
voilà où je me suis arrêtée ! Merci pour votre réponse 
Bonjour Glapion ; ce n'est pas tant que c'est "plus facile", c'est surtout moins faux ! Et idem pour MC²= MA²+AC²-2 MA.AC.cos(MAC).
D'accord, Vax (à part la question 1, bien sûr)
Pour 4) et 5), continue à penser à Al Kashi, Pythagore, Al Kashi ...
je viens de m'apercevoir d'une petite incohérence dans mon tableau de variation, sur [15;+] f'(x) est négative donc f(x) est décroissante; or f(15)=0.77143 et la limite en + est 1.
3) b. Comment arrive-t-on à M1B=rac(7) ? je pensais poser une équation du type f(x)=1 et trouver MB²=... et en déduire sa valeur, mais je n'y arrive pas
Merci d'avance !
j'ai retrouvé les valeurs de la question 3b).
4. En utilisant Al-Kashi j'ai trouvé BC²=49 d'où BC=7.
5. a) cos()= (M1B²-BC²-M1C²)/(-2.BC.MC) = 63/(2.rac(7).rac(21))
Je ne sais pas réduire pour arriver à 9/2.rac(21).
b) cos()= (CM1²-AC²-AM1²)/(-2.AC.AM1)=1/5 . Je pense m'être trompée car je ne vois â le lien avec la question suivante.
c) je pensais faire cos()= cos() donc = et M appartient à la bissectrice.
je bloque pour la suite...
J'ai néanmoins réussi à répondre à la question 8)a (TVI qui montre une unique solution), et b MB=MC or M est variable; donc un seul point possible pour que M soit équidistant de B et C.
merci d'avance pour votre réponse
5a)b)c) : écris Al Kashi correctement et exploite-le sans faire d'erreurs de calcul (tu devrais éviter de proposer des valeurs de cosinus égales à 2,598 ...)
En fait c'est bon j'ai réussi à répondre entièrement à la question 5.
Pourriez m'indiquer comment je peux prouver que le triangle M1BM2 est rectangle ? j'ai essayé avec le théorème de Pythagore mais je n'ai pas la valeurs de M1M2²...
Bonjour à tous,
En cherchant à refaire cet exercice, je bloque sur deux points :
- le 6°c sur quelles droites remarquables se situe M2?
- le 8°b justifier géométriquement ce résultat.
Les "droites remarquables" me laisse songeur et je vois bien que le triangle BMoC est isocèle en Mo puisque le rapport BMo²/CMo² est égal à 1 pour la valeur xo=8, mais par quel moyen puis-je en faire la démonstration géométrique ?
L'égalité des angles MoBC et MoCB ?
Je vous remercie par avance.
Bonjour
M1 appartient à la bissectrice de ACB => M1 est le centre du cercle inscrit à ABC
6)a)b) =>
M2CM1 =90° et M2BM1 = 90°donc
6°c) M2 appartient à la perpendiculaire à CM1 en C et M2 appartient à la perpendiculaire à BM1 en B
8°b)comme BMo²/CMo² est égal à 1 pour la valeur xo=8 Mo appartient à la médiatrice de BC
et M2 appartient aussi au cercle circonscrit à M1BC ( de diamètre M1M2 et de centre Mo) et aussi par hypothèse à la bissectrice de BAC
A+
Je te remercie beaucoup pour le coup de main et les explications détaillées. je trouve le problème intéressant dans la mesure où il renvoie, me semble-t-il à des définitions acquises au collège, ou même avant, et dont il faut se souvenir comme ici la médiatrice, et à des outils comme la relation d'Al Kashi.
A bientôt.
Annuler
connectez vous