Inscription / Connexion Nouveau Sujet
DM de maths
Bonjour, j'ai un DM de maths à faire mais il y a un exercice qui me pose problème. J'espère que vous pourrez m'aider. Voici mon énoncé:
" Dans un tronc d'arbre circulaire de rayon R, on découpe une poutre en forme de parallélépipède rectangle. On cherche la longueur et a hauteur de la poutre lui assurant la plus grande résistance possible.
On admet en première approximation que la résistance à la compression est maximale quand l'aire de la section est maximale. On note
la mesure en radians de l'angle marqué tel que 0
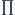/2.
1_ Exprimer la longueur l et la hauteur h en fonction de R et .
2_Montrer que l'aire de la section ABCD est donnée en fonction de par A()=2R^2 sin^2(2)
3_Etudier le sens de variationde A sur [0;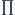/2]
4_En déduire la valeur de pour laquelle la poutre résiste le mieux à la pression.
Je vous remercie d'avance pour votre aide.
je trouve h= 2Rsin() et l= 2Rcos() en me plaçant dans des triangles et en utilisant le sin et le cos.
Mais pour la question suivante je n'arrive pas à A()=2R²sin²(2), je reste bloquée à l*h= 2*2*R*R*Cos()Sin()
Si vous pouviez m'expliquer
Si tu compares ce que tu obtiens avec ce que tu dois obtenir, il te suffit de montrer que :
sin(2a) = 2.sin(a).cos(a)
N'est-ce pas une question de cours ?
Bonjour
oui c'est bien une erreur,cela a été confirmé par ma prof...
Donc si quelqu'un pouvait m'aider pour la question suivante: Etudier le sens de variation de A sur [0;
/2]
Je ne comprends pas comment faire
Merci d'avance
Les variations de la fonction "sinus" sur [0;pi] sont une question de cours.
Les variations de A s'en déduisent immédiatement.
Je ne pense pas.
Quelles sont les variations de x |--> sin(x) sur [0;pi] ?
Donc quelles sont les variations de x |--> sin(2x) sur [0;pi/2] ?
les variations de x |--> sin(x) sur [0;pi] sont croissant sur [0;/2] et decroissant sur [/2; ]
Mais après je ne sais pas comment faire
"sin(x)" est croissante pour x dans [0;pi/2] puis décroissante pour x dans [pi/2;pi]
On remplace x par 2x :
"sin(2x)" est croissante pour 2x dans [0;pi/2] puis décroissante pour 2x dans [pi/2;pi]
C'est-à-dire :
"sin(2x)" est croissante pour x dans [0;pi/4] puis décroissante pour x dans [pi/4;pi/2]
merci j'ai compris maintenant.
Donc pour la question 4, j'en déduis que l'angle doit etre /4 en le justifiant avec mon tableau de variation, c'est ça?
Comme x |--> sin(x) sur [0;pi] est croissant sur [0;pi/2] et décroissant sur [pi/2;0]
Je peux dire que les variations de x |--> sin(2x) sur [0;pi] sont croissantes sur [0;pi/2] et décroissantes sur [pi/2;0] .
Alors 2R^2sin(2x) est croissant sur [0;pi/2] (comme 2R^2 >0 et sin(2x) croissant sur [0;pi/2])
C'est çà ??
Si vous pouviez m'aider pour une derniere chose sur cet meme exercice....
On sait que h=
(4R^2-l^2)
J'ai trouvé l=2R3/3
Alors h=4R^2-2R3/3^2
Je n'arrive pas à continuer...
Ah pardon, non mais c'est parce que c'est la partie B de l'exo:
On admet que la résistance à la flexion varie comme le produit lh²
1/ Exprimer h en fonction de R et l
2/ En déduire que lh² = -l^3 + 4R²l
3/ Soit f(x) = x^3 + 4R²x
a)Etudier les variations de la fonction f sur R
b)Comment choisir l et h pour que la poutre résiste le mieux à la flexion ?
4/ Quel est l'angle correspondant ? (arrondir à 0,1° près)
J'ai donc tout trouvé sauf la 3b et comme je vous l'ai dit j'ai trouvé l et maintenant je dois trouver h avec le calcul ecrit dans mon dernier post
Une version interactive et dynamique de l'image ci-dessus est disponible au bout du lien suivant : http://www.geogebratube.org/student/m102600
(déplacer le curseur en haut à droite avec la souris et la figure s'adapte automatiquement)
Annuler
connectez vous