Inscription / Connexion Nouveau Sujet
Construction de polygones
Mon problème est de construire matériellement des polygones. Je ne suis pas mathématicien (et je le regrette!) et je dois donc tracer mes polygones. Pour le carré ou le penta, pas de problèmes, un compas suffit. Mais quand il s'agit de tracer un heptagone c'est très compliqué. J'ai consulté tous les sites que j'ai pu sur Wiki et je n'ai rien trouvé de satisfaisant.
J'ai donc travaillé de manière intuitive et j'ai trouvé ! Même pas besoin de tracer, un simple calcul suffit : Il me faut 7 triangles réunis par le sommet, soit 360 : 7 = 51.428571°, si je divise par 2 j'obtiens 25.714285°.(On obtient le même résultat en divisant 360 par 14, puisqu'il y à 2x7 extémités)
Là je rejoins mon atelier et j'affiche cette valeur sur ma scie à onglets (coup d'oeil et maîtrise de la machine obligatoire), puis je coupe 7 segments de longueurs égales avec ce même angle à chaque extrémité(inversés).
Et là lorsque je superpose mes 14 demi-angles j'obtiens immédiatement un heptagone (ou un héptaèdre puisqu'il y a une hauteur) parfait.
Si cette solution intéresse un matheux, je serai curieux de savoir si on peut en faire une démonstration géométrique.
Bonjour ,
la méthode proposée revient à utiliser un rapporteur .
Il n'existe que des méthodes approchées pour obtenir un heptagone avec seulement la règle et le compas .
Une des méthodes les plus précises (1/1000) est donnée sur http://www.geogebratube.org/student/m15417
Cordialement
Bonjour,
un heptagone (ou un héptaèdre puisqu'il y a une hauteur)
un heptaèdre a par définition 7 faces en tout, pas une face avec 7 arêtes.
sinon :
1) on ne peut construire (à la règle et au compas) que les polygones réguliers à nombre de côtés 2n
pqr... où p, q, r ... sont des nombres premiers de Fermat (de la forme on n'en connait que 5 : 3, 5, 17, 257, 65537
de sorte que la proposition revient, tant qu'on n'a pas trouvé d'autres nombres premiers de Fermat, à :
le polygone est constructible si et seulement si il a 2n
P côtés avec P diviseur de 232 - 1 = 4294967295
une proposition équivalente est : ssi la fonction d'Euler
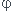(N) est une puissance de 2.
Si le nombre de côtés contient un autre facteur premier, ou une puissance supérieure des nombres premiers de Fermat, par exemple 7, 9, 11, 13, 25, etc
on ne peut pas le construire à la règle et au compas.
2) si on dispose d'autres instruments, c'est possible
par exemple si on dispose d'un trisecteur (instrument permettant de diviser un angle quelconque en 3) ou d'un instrument capable de tracer d'un trait continu une conique quelconque, on peut étendre la construction à tous les polygones de 2n
3m
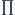p ou les p sont des nombres premiers de la forme 2a3b + 1 distincts
Ainsi les polygones à 7 et 13 cotés deviennent constructibles, ainsi que le polygone à 9 cotés (3
3) et 360 côtés (23325)
le polygone à 11 côtés n'est toujours pas constructible.
Diverses méthodes de trisection de l'angle (par exemple un tomahawk, ou par les origami) par exemple là :
pour la construction pratique de trisecteurs.
Ca fait un peu bidouille (c'est le nom du site)
La construction d'un heptagone exact avec un trisecteur peut être par exemple :
On construit le triangle équilatéral OBC avec OB = OA/2
puis on reporte cette distance OI = OC et CD = DF = BC
L'angle FID est ensuite trisecté et les trois trisectrices (de même qu'un angle a deux bisectrices, il a trois trisectrices) coupent l'axe OA en H, K et L.
les perpendiculaires à OA en H,K,L donnent les sommets de l'heptagone inscrit.
3) On trouve des constructions approchées plus ou moins astucieuses (celle donnée par geogebratube est super simple !!)
l'usage d'un rapporteur ou d'un équivallent par calcul et report d'une longueur calculée est une construction approchée
Geogebra lui-même si on lui demande de construire un heptagone régulier le fait de façon approchée (en calculant l'angle et les sinus et cosinus de cet angle pour opérer la rotation par les formules de rotation habituelles) Il fait d'ailleurs pareil pour tous les polygones (son compas est fait par calculs approchés même !)
une aproximation à 10-15 près, c'est tout de même pas mal !
Les autres logiciels de DAO ou de CAO sont capables de faire pareil. De sorte qu'il n'y a aucun état d'ame à avoir pour demander au logiciel de CAO de tracer un heptagone et de faire usiner les pièces correspondantes.
Même pour un polygone constructible (un pentagone par ex) ce sera plus précis "par calcul" et machine outil qu'en traçant avec un vrai compas physique !
Et cumuler les erreurs de calculs en "construisant géométriquement à la règle et au compas" en DAO/CAO est une aberration ! le compas d'un logiciel DAO/CAO n'a que peu de rapport avec un compas "mathématique".
Annuler
connectez vous