Fiche de mathématiques
Ile mathématiques > maths bac > Bac 2023 toujours : des sujets venus d'ailleurs
Bac Mathématiques
Durée : 4h
Coefficient: 5
3 points
On donne dans l'espace muni d'un repère orthonormé \text{ les points } A(1;1;1)\text{ ; }B(-1;2;0)\text{ et }C(3;0;1)) .
.
1-a) Calculer le produit vectoriel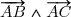 .
.
b) En déduire qu'une équation du plan) passant par les points
passant par les points 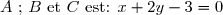
2) Soit) l'ensemble des points
l'ensemble des points ) de l'espace tel que:
de l'espace tel que: 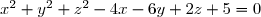 .
.
Montrer que) est une sphère de centre
est une sphère de centre ) et de rayon
et de rayon 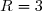 .
.
3-a) Déterminer une représentation paramétrique de la droite) passant par
passant par 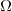 et orthogonale au plan
et orthogonale au plan  ) .
.
b) Déterminer les coordonnées du point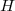 intersection de la droite
intersection de la droite ) et du plan
et du plan ) .
.
4) montrer que la sphère) et le plan
et le plan ) se coupent suivant un cercle dont on déterminera le centre et le rayon.
se coupent suivant un cercle dont on déterminera le centre et le rayon.
3 points
 et
et 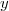 sont des entiers naturels.
sont des entiers naturels.
Une urne contient boules blanches et
boules blanches et 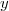 boules rouges indiscernables au toucher.
boules rouges indiscernables au toucher.
On considère le système\text{ : }\begin{cases} (2x+y)(7x+5y)=765\\ pgcd(x;y)=3\end{cases}) .
.
1-a) Décomposer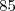 en produit des facteurs premiers.
en produit des facteurs premiers.
b) Déterminer l'ensemble des diviseurs positifs de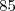 .
.
c) Résoudre dans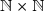 le système
le système ) .
.
2) Dans cette question on suppose que l'urne contient trois boules blanches et six boules rouges.
On tire simultanément et au hasard deux boules de l'urne.
Soit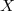 la variable aléatoire désignant le nombre des boules blanches tirées.
la variable aléatoire désignant le nombre des boules blanches tirées.
a) Déterminer la loi de probabilité de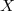 .
.
b) Calculer l'espérance et la variance de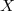 .
.
6 points
1-a) Résoudre dans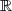 l'équation différentielle
l'équation différentielle \text{ : }y''+y=0) .
.
b) Déterminer les solutions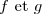 de l'équation
de l'équation ) telles que:
telles que: =1\text{ et }f\left(\dfrac{\pi}{2}\right)=0\text{ , puis } g(0)=0\text{ et }g\left(\dfrac{\pi}{2}\right)=2)
2) Soit) la courbe paramétrée définie par:
la courbe paramétrée définie par: =\cos t \\y(t)=2\in t \end{cases}\text{ , }(t\in\R))
a) Étudier la position des points\text{ et }M(-t) ) puis celle des points
puis celle des points \text{ et }M(t)) .
.
b) En déduire que l'on peut étudier) sur l'intervalle
sur l'intervalle ![[0;\pi]](https://latex.ilemaths.net/latex-0.tex?[0;\pi]) .
.
c) Calculer\text{ et }y'(t)) dérivées des fonctions
dérivées des fonctions \text{ et }y(t)) .
.
d) Préciser les vecteurs dérivées aux points\text{ , }M_1\left(t=\dfrac{\pi}{2}\right)\text{ et }M_2(t=\pi)) .
.
e) Dresser le tableau de variation commun de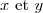 .
.
f) Construire) dans le repère orthonormé
dans le repère orthonormé ) .
.
3-a) Montrer qu'une équation réduite de) est:
est: 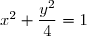
b) Déterminer la nature et les éléments caractéristiques de) (centre, foyers, sommets et directrices) .
(centre, foyers, sommets et directrices) .
4) L'aire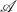 de
de ) en unité d'aire est donnée par:
en unité d'aire est donnée par: \times y(t)\text{ d}t) .
.
a) Montrer que\text{ d}t) .
.
b) Déterminer la valeur exacte de=\dfrac{1-\cos(2t)}{2} \right))
8 points
Partie A: Étude d'une fonction
On appelle la fonction définie sur
la fonction définie sur 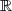 par :
par : =\ln(x^2+x+1) \text{ ; }(C)) sa courbe représentative dans un repère orthonormé
sa courbe représentative dans un repère orthonormé ) .
.
1) Calculer les limites de en
en 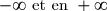 .
.
2-a) Vérifier que}{x}=\dfrac{2\ln x}{x}+\dfrac{1}{x}\times \ln\left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right) ) .
.
b) En déduire}{x}) . Interpréter graphiquement le résultat.
. Interpréter graphiquement le résultat.
3-a) Justifier que est dérivable sur
est dérivable sur 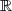 puis montrer que
puis montrer que =\dfrac{2x+1}{x^2+x+1}) .
.
b) Dresser le tableau de variation de .
.
4) Déterminer une équation de la tangente) à la courbe
à la courbe 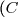) de
de  en
en 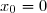 .
.
5) On considère la fonction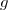 définie sur
définie sur 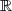 par :
par : =f(x)-x) .
.
a) Justifier que=-\infty\text{ , puis calculer }\lim_{x\to-\infty} g(x)) .
.
b) Calculer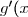) puis dresser le tableau de variation de
puis dresser le tableau de variation de 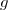 .
.
c) Montrer que l'équation=0) admet sur
admet sur 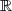 deux solutions :
deux solutions : 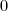 et une autre, notée
et une autre, notée ![\alpha\in\left[\dfrac{3}{2};2\right]](https://latex.ilemaths.net/latex-0.tex?\alpha\in\left[\dfrac{3}{2};2\right]) .
.
d) En déduire suivant les valeurs de le signe de
le signe de ) . Préciser la position de la courbe
. Préciser la position de la courbe 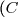) par rapport à
par rapport à ) .
.
6) On admet qu'en) admet une branche parabolique de direction l'axe des abscisses ; Construire
admet une branche parabolique de direction l'axe des abscisses ; Construire \text{ et }(C)) dans un repère orthonormé
dans un repère orthonormé ) .
.
Partie B: Étude d'une suite récurrente
On appelle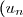) la suite définie sur
la suite définie sur 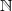 par:
par:  \end{cases})
1-a) Montrer par récurrence que: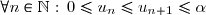 .
.
b) En déduire que la suite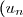) converge.
converge.
2) Montrer que|\leq \dfrac{16}{19}) . (On pourra étudier le signe de
. (On pourra étudier le signe de -\dfrac{16}{19})
 )
)
3-a) Montrer que\text{ d}x\right|\leq \dfrac{16}{19} |u_n-\alpha| ) .
.
b) En déduire que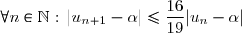 .
.
c) En déduire que^n ) .
.
d) Quelle est la limite de la suite ) ?
?
e) Déterminer le plus petit entier naturel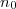 tel que
tel que 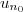 soit une valeur approchée de
soit une valeur approchée de  à
à  .Publié par malou/Panter
le
.Publié par malou/Panter
le
Bac Mathématiques
Union des Comores 2023
Série C
Coefficient: 5
3 points
exercice 1
On donne dans l'espace muni d'un repère orthonormé
1-a) Calculer le produit vectoriel
b) En déduire qu'une équation du plan
2) Soit
Montrer que
3-a) Déterminer une représentation paramétrique de la droite
b) Déterminer les coordonnées du point
4) montrer que la sphère
3 points
exercice 2
Une urne contient
On considère le système
1-a) Décomposer
b) Déterminer l'ensemble des diviseurs positifs de
c) Résoudre dans
2) Dans cette question on suppose que l'urne contient trois boules blanches et six boules rouges.
On tire simultanément et au hasard deux boules de l'urne.
Soit
a) Déterminer la loi de probabilité de
b) Calculer l'espérance et la variance de
6 points
exercice 3
1-a) Résoudre dans
b) Déterminer les solutions
2) Soit
a) Étudier la position des points
b) En déduire que l'on peut étudier
c) Calculer
d) Préciser les vecteurs dérivées aux points
e) Dresser le tableau de variation commun de
f) Construire
3-a) Montrer qu'une équation réduite de
b) Déterminer la nature et les éléments caractéristiques de
4) L'aire
a) Montrer que
b) Déterminer la valeur exacte de
8 points
probleme
Partie A: Étude d'une fonction
On appelle
1) Calculer les limites de
2-a) Vérifier que
b) En déduire
3-a) Justifier que
b) Dresser le tableau de variation de
4) Déterminer une équation de la tangente
5) On considère la fonction
a) Justifier que
b) Calculer
c) Montrer que l'équation
d) En déduire suivant les valeurs de
6) On admet qu'en
Partie B: Étude d'une suite récurrente
On appelle
1-a) Montrer par récurrence que:
b) En déduire que la suite
2) Montrer que
3-a) Montrer que
b) En déduire que
c) En déduire que
d) Quelle est la limite de la suite
e) Déterminer le plus petit entier naturel
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 forum de terminale
forum de terminale