Fiche de mathématiques
Ile mathématiques > maths bac > Bac 2023 toujours : des sujets venus d'ailleurs
Bac Mathématiques
Durée : 4h
Coefficient: 5
Calculatrice non autorisée
4 points

4 points

12 points


A)
1) On a pour tout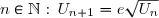
Donc: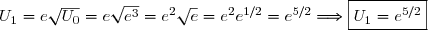
Montrons que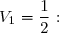
On a: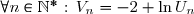
Donc:=-2+\dfrac{5}{2}=\dfrac{1}{2} \Longrightarrow \boxed{V_1=\dfrac{1}{2}} )
2) On a, pour tout
\\\\&=&-2+\ln e+\ln(U_n^{1/2})&=&-2+1+\dfrac{1}{2} \ln U_n \\\\&=& \dfrac{1}{2}(-2+\ln U_n)&=&\dfrac{1}{2} V_n\end{matrix})
Donc: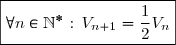
On en déduit que:\text{ est géométrique de raison }\dfrac{1}{2}})
3-a) La suite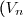) est une suite géoémtrique de raison
est une suite géoémtrique de raison  est de premier terme
est de premier terme 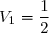 .
.
D'où:
^{n-1} \Longrightarrow \forall n\in\N^*\text{ : }V_n=\dfrac{1}{2} \left(\dfrac{1}{2}\right)^{n-1}\Longrightarrow \boxed{\forall n\in \N^*\text{ : }V_n=\left(\dfrac 12\right)^n })
b) On a:
^n+2})
On obtient:^n+2})
De plus:^0+2}=e^{1+2}=e^3=U_0)
On en tire que:^n+2 }})
c) Puisque^n=0) , il s'ensuit que :
, il s'ensuit que :
^n+2}=e^{0+2}=e^2 \Longrightarrow \boxed{\displaystyle\lim_{n\to +\infty} U_n=e^2})
B)
1) On a-e^x}{1+e^x}=\dfrac{e^x+e^{2x}-e^x}{1+e^x}=\dfrac{e^{2x}}{1+e^x})
Donc: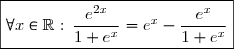
2) Calculons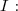
![\begin{matrix} I&=& \displaystyle \int_0^1 \dfrac{e^{2x}}{1+e^x}\text{ d}x &=& \displaystyle \int_0^1 e^x-\dfrac{e^x}{1+e^x}\text{ d}x &=& \displaystyle \int_0^1 \left(e^x\right)'-\dfrac{\left(1+e^x\right)'}{1+e^x}\text{ d}x \\\\ &=& \left[ e^x-\ln \left|1+e^x \right|\right]_0^1 &=& \underbrace{\left[ e^x-\ln \left(1+e^x \right)\right]_0^1}_{\text{ Car: }\forall x\in[0;1]\text{ : } 1+e^x>0 } &=& e-\ln(1+e)-1+\ln 2 \\\\&=& e-1+\ln\left(\dfrac{2}{1+e}\right)\end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} I&=& \displaystyle \int_0^1 \dfrac{e^{2x}}{1+e^x}\text{ d}x &=& \displaystyle \int_0^1 e^x-\dfrac{e^x}{1+e^x}\text{ d}x &=& \displaystyle \int_0^1 \left(e^x\right)'-\dfrac{\left(1+e^x\right)'}{1+e^x}\text{ d}x \\\\ &=& \left[ e^x-\ln \left|1+e^x \right|\right]_0^1 &=& \underbrace{\left[ e^x-\ln \left(1+e^x \right)\right]_0^1}_{\text{ Car: }\forall x\in[0;1]\text{ : } 1+e^x>0 } &=& e-\ln(1+e)-1+\ln 2 \\\\&=& e-1+\ln\left(\dfrac{2}{1+e}\right)\end{matrix} )
})
\text{ : }y'-2y=x^2)
1) Soit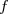 une fonction définie par
une fonction définie par =ax^2+bx+c\text{ tels que }a,b,c\in\R) .
.
 &\iff& \forall x\in\R\text{ : }f'(x)-2f(x)=x^2 \\\\&\iff& \forall x\in\R\text{ : } 2ax+b-2ax^2-2bx-2c=x^2 \\\\&\iff& \forall x\in\R\text{ : }-2ax^2+(2a-2b)x+b-2c=0 \\\\&\iff& \begin{cases} -2a=1 \\2a-2b=0 \\b-2c=0 \end{cases}\\\\&\iff& \begin{cases} a=-\dfrac{1}{2} \\ b=-\dfrac{1}{2} \\ c=\dfrac{b}{2}=-\dfrac{1}{4}\end{cases} \end{matrix} )
Donc:
=-\dfrac{1}{2}\left(x^2+x+\dfrac{1}{2}\right) \text{ est solution de l'équation }(E) })
2) L'équation différentielle\text{ : }y'-2y=0) est une équation différentielle du premier degré à coefficients constants et sans second membre.
est une équation différentielle du premier degré à coefficients constants et sans second membre.
Donc les solutions de) s'écrivent:
s'écrivent: x}=ke^{2x} \text{ / } k\in\R )
L'ensemble des solutions de) est:
est:
}=\left\lbrace x\mapsto ke^{2x} \text{/ }k\in\R \right\rbrace })
3) Soit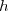 une fonction définie et dérivable sur
une fonction définie et dérivable sur 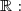
 &\iff& (h-f)'-2(h-f)=0 \\&\iff& h'-f'-2h-2f=0 \\&\iff& h'-2h=f'-2f \\&\iff& h'-2h=x^2 &\enskip\text{ car }f\text{est une solution de l'équation }(E) \\&\iff& h\text{ est solution de }(E) \end{matrix} )
 \text{ si et seulement si }h\text{ est solution de }(E) })
4) Soit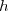 solution de
solution de ) , donc
, donc  est solution de
est solution de ) .
.
On en tire que:
(x)=ke^{2x} \text{ / }k\in\R &\iff& \forall x\in\R\text{ : }h(x)-f(x)=ke^{2x}\text{ / }k\in\R \\\\&\iff& h(x)=ke^{2x}+f(x)\text{ / } k\in\R \\\\&\iff& h(x)= ke^{2x}-\dfrac{1}{2}\left(x^2+x+\dfrac{1}{2}\right) \text{ / }k\in\R\end{matrix})
L'ensemble des solutions de) est:
est:
}=\left\lbrace x\mapsto ke^{2x}-\dfrac{1}{2}\left(x^2+x+\dfrac{1}{2}\right) \text{/ }k\in\R \right\rbrace })
5)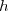 est solution de
est solution de ) vérifiant
vérifiant =\dfrac{3}{4}) , donc il existe
, donc il existe =ke^{2x}-\dfrac{1}{2}\left(x^2+x+\dfrac{1}{2}\right))
Il s'ensuit:=\dfrac{3}{4} &\iff& ke^0-\dfrac{1}{2}\times \dfrac{1}{2} =\dfrac{3}{4} &\iff& k=\dfrac{3}{4}+\dfrac{1}{4} = 1 \end{matrix} )
=e^{2x}-\dfrac{1}{2}\left(x^2+x+\dfrac{1}{2}\right)})
Partie A:
![\forall x\in]0;+\infty[\text{ : }g(x)=x^2+1-\ln x](https://latex.ilemaths.net/latex-0.tex?\forall x\in]0;+\infty[\text{ : }g(x)=x^2+1-\ln x)
![\forall x\in]0;+\infty[\text{ : }f(x)=x+1+\dfrac{\ln x}{x}](https://latex.ilemaths.net/latex-0.tex?\forall x\in]0;+\infty[\text{ : }f(x)=x+1+\dfrac{\ln x}{x})
1) La fonction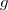 est dérivable sur
est dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[ ) comme somme de fonctions dérivables sur cet intervalle.
comme somme de fonctions dérivables sur cet intervalle.
![\begin{matrix} \forall x\in ]0;+\infty[\text{ : }g'(x)&=& (x^2+1-\ln x)'&=& 2x-\dfrac{1}{x} &=& \dfrac{2x^2-1}{x} \end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} \forall x\in ]0;+\infty[\text{ : }g'(x)&=& (x^2+1-\ln x)'&=& 2x-\dfrac{1}{x} &=& \dfrac{2x^2-1}{x} \end{matrix})
![\boxed{\forall x\in ]0;+\infty[\text{ : }g'(x)=\dfrac{2x^2-1}{x}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in ]0;+\infty[\text{ : }g'(x)=\dfrac{2x^2-1}{x}})
Étude de signe:
On sait que:![\forall x\in]0;+\infty[\text{ : }g'(x)=\dfrac{2x^2-1}{x}=\dfrac{(\sqrt{2}x)^2-1}{x}=\dfrac{(\sqrt{2} x-1)(\sqrt{2}+1)}{x}](https://latex.ilemaths.net/latex-0.tex?\forall x\in]0;+\infty[\text{ : }g'(x)=\dfrac{2x^2-1}{x}=\dfrac{(\sqrt{2}x)^2-1}{x}=\dfrac{(\sqrt{2} x-1)(\sqrt{2}+1)}{x})
Or,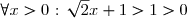 . Donc le signe de
. Donc le signe de 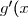) est celui de
est celui de 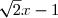 , qui est un polynôme de premier degré qui s'annule en
, qui est un polynôme de premier degré qui s'annule en 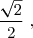 en effet :
en effet :
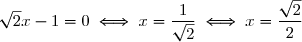
Dressons le tableau de signe:
 & \dbarre & - & \barre{0} &+& \\ \hline \end{array}} )
On conclut alors que:
![\boxed{\begin{matrix} \forall x\in \left]0;\dfrac{\sqrt{2}}{2}\right[ \text{ : } & g'(x)<0 \\ g'\left(\dfrac{\sqrt{2}}{2}\right)=0 &\\ \forall x\in \left]\dfrac{\sqrt{2}}{2};+\infty[ \text{ : } &g'(x)>0 \end{matrix} }](https://latex.ilemaths.net/latex-0.tex?\boxed{\begin{matrix} \forall x\in \left]0;\dfrac{\sqrt{2}}{2}\right[ \text{ : } & g'(x)<0 \\ g'\left(\dfrac{\sqrt{2}}{2}\right)=0 &\\ \forall x\in \left]\dfrac{\sqrt{2}}{2};+\infty[ \text{ : } &g'(x)>0 \end{matrix} } )
2) Calculons\text{ : })
=\left(\dfrac{\sqrt{2}}{2}\right)^2+1-\ln\left(\dfrac{\sqrt{2}}{2}\right) = \dfrac{2}{4}+1-\ln \sqrt{2}+\ln 2 =\dfrac{1}{2}+1-\dfrac{1}{2}\ln 2+\ln 2=\dfrac{3}{2}+\dfrac{\ln 2}{2} )
=\frac{1}{2}(\ln 2+3)})
Ayant étudié le signe de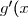) , on peut dresser le tableau de variations de la fonction
, on peut dresser le tableau de variations de la fonction 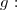
 & \dbarre & - & \barre{0} &+& \\ \hline & \dbarre&&&& \\ g & \dbarre & \searrow & & \nearrow & \\ &\dbarre & &(\ln 2+3)/2&& \\ &\dbarre & &&& \\ \hline \end{array}} )
On en tire que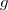 amdet un minimum
amdet un minimum 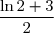 en
en 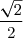 sur
sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) .
.
Donc:![\forall x\in ]0;+\infty[\text{ : }g(x)\geq \dfrac{\ln 2+3}{2}](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]0;+\infty[\text{ : }g(x)\geq \dfrac{\ln 2+3}{2})
Finalement: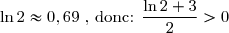
D'où:![\boxed{\forall x\in ]0;+\infty[\text{ : }g(x)>0 }](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in ]0;+\infty[\text{ : }g(x)>0 })
3)
Calcul des limites:
= \lim_{x\to 0^+} x+1+\dfrac{\ln x}{x} = \lim_{x\to 0^+} x+1+\ln x \times \dfrac{1}{x}= 0+1+(-\infty)\times (+\infty)=-\infty)
=-\infty})
Interprétation graphique:
 })
= \lim_{x\to +\infty} x+1+\dfrac{\ln x}{x} = (+\infty)+1+0=+\infty)
=+\infty})
4-a) La fonction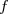 est dérivable sur
est dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) comme somme de fonctions dérivables sur
comme somme de fonctions dérivables sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[)
![\forall x\in ]0;+\infty[\text{ : }f'(x)=\left(x+1+\dfrac{\ln x}{x}\right)'=1+\dfrac{(\ln x)'x-\ln x}{x^2}=1+\dfrac{1-\ln x}{x^2}](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]0;+\infty[\text{ : }f'(x)=\left(x+1+\dfrac{\ln x}{x}\right)'=1+\dfrac{(\ln x)'x-\ln x}{x^2}=1+\dfrac{1-\ln x}{x^2})
![\boxed{\forall x\in ]0;+\infty[\text{ : }f'(x)=1+\dfrac{1-\ln x}{x^2}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in ]0;+\infty[\text{ : }f'(x)=1+\dfrac{1-\ln x}{x^2}})
Vérification:
![\forall x\in ]0;+\infty[\text{ : } f'(x)=1+\dfrac{1-\ln x}{x^2}=\dfrac{x^2+1-\ln x}{x^2}=\dfrac{g(x)}{x^2} \enskip\enskip \Longrightarrow \enskip\enskip \boxed{\forall x\in ]0;+\infty[\text{ : }f'(x)=\frac{g(x)}{x^2}}](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]0;+\infty[\text{ : } f'(x)=1+\dfrac{1-\ln x}{x^2}=\dfrac{x^2+1-\ln x}{x^2}=\dfrac{g(x)}{x^2} \enskip\enskip \Longrightarrow \enskip\enskip \boxed{\forall x\in ]0;+\infty[\text{ : }f'(x)=\frac{g(x)}{x^2}} )
b) D'après ce qui précède, la fonction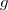 est strictement positive sur
est strictement positive sur 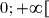 .
.
De plus,![\forall x \in]0;+\infty[\text{ : }x^2>0](https://latex.ilemaths.net/latex-0.tex?\forall x \in]0;+\infty[\text{ : }x^2>0)
On obtient alors:![\boxed{\forall x\in ]0;+\infty[\text{ : }f'(x)>0 }](https://latex.ilemaths.net/latex-0.tex?\boxed{\forall x\in ]0;+\infty[\text{ : }f'(x)>0 })
Et on dresse le tableau de variations de la fonction
 & \dbarre& & +& \\ \hline & \dbarre& & & +\infty \\ f & \dbarre & & \nearrow & \\ &\dbarre & 0&& \\ \hline \end{array}} )
c) La fonction est continue sur
est continue sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) car elle est dérivable sur cet intervalle.
car elle est dérivable sur cet intervalle.
De plus, est strictement croissante sur
est strictement croissante sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) .
.
Et puisque=-\infty\text{ et }\displaystyle\lim_{x\to +\infty} f(x)=+\infty) , alors
, alors ![f(]0;+\infty[)=]-\infty;+\infty[=\R](https://latex.ilemaths.net/latex-0.tex?f(]0;+\infty[)=]-\infty;+\infty[=\R)
On en tire que![0\in f(]0;+\infty[)](https://latex.ilemaths.net/latex-0.tex?0\in f(]0;+\infty[)) et donc, d'après le théorème des valeurs intermédiaires:
et donc, d'après le théorème des valeurs intermédiaires:
![\boxed{\text{L'équation }f(x)=0\text{ amdet une solution unique notée }\alpha\text{sur }]0;+\infty[}](https://latex.ilemaths.net/latex-0.tex?\boxed{\text{L'équation }f(x)=0\text{ amdet une solution unique notée }\alpha\text{sur }]0;+\infty[})
Encadrement de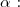
=\dfrac{1}{4}+1+\dfrac{\ln (1/4)}{1/4}=\dfrac{5}{4}-4\ln 4=\dfrac{5}{4}-8\ln 2<0\enskip\enskip\text{ puisque }\dfrac 5 4 =1,25 \text{ et }\ln 2\approx 0,69\text{, donc }8\ln 2 >4)
=\dfrac{1}{2}+1+\dfrac{\ln (1/2)}{1/2}=\dfrac{3}{2}-2\ln 2>0\enskip\enskip\text{ puisque }\dfrac 3 2 =1,5 \text{ et }\ln 2\approx 0,69\text{ , donc } 2\ln 2 \approx 1,4)
On en déduit que :\leq f(\alpha)=0\leq f\left(\dfrac{1}{2}\right))
Et en sachant que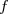 est strictement croissante sur
est strictement croissante sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) , on conclut que:
, on conclut que:
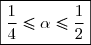
5) Soit\text{ : }y=x+1) . On a:
. On a:
-y = \displaystyle\lim_{x\to +\infty} x+1+\dfrac{\ln x}{x}-(x+1) = \displaystyle\lim_{x\to +\infty} \dfrac{\ln x}{x}=0)
Interprétation graphique:
\text{ : }y=x+1 \text{ est une asymptote oblique à la courbe }(\mathscr{C})\text{ au voisinage de }+\infty } )
Étude de la position relative:
Étudions le signe de-y \text{ , on a :})
![\forall x\in ]0;+\infty[\text{ : }f(x)-y=\dfrac{\ln x}{x}](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]0;+\infty[\text{ : }f(x)-y=\dfrac{\ln x}{x}) , donc le signe de
, donc le signe de -y) est celui de
est celui de 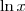 .
.
Et puisque:![\begin{cases} \forall x\in ]0;1[\text{ : }\ln x<0 \\ \ln 1 = 0 \\ \forall x\in ]1;+\infty[\text{ : }\ln x>0 \end{cases} \enskip\enskip\Longrightarrow \enskip\enskip \begin{cases} \forall x\in ]0;1[\text{ : }f(x)-y<0 \\ \text{ Si }x=1\text{ : }f(x) = y \\ \forall x\in ]1;+\infty[\text{ : }f(x)-y>0 \end{cases}](https://latex.ilemaths.net/latex-0.tex?\begin{cases} \forall x\in ]0;1[\text{ : }\ln x<0 \\ \ln 1 = 0 \\ \forall x\in ]1;+\infty[\text{ : }\ln x>0 \end{cases} \enskip\enskip\Longrightarrow \enskip\enskip \begin{cases} \forall x\in ]0;1[\text{ : }f(x)-y<0 \\ \text{ Si }x=1\text{ : }f(x) = y \\ \forall x\in ]1;+\infty[\text{ : }f(x)-y>0 \end{cases} )
Finalement, si=y\Longrightarrow f(1)=1+1=2)
On en déduit que:
![\boxed{\begin{matrix} \bullet & (\mathscr{C}) \text{ est en dessous de la droite }(\Delta) \text{ sur l'intervalle }\left]0;1\right[ \\ \bullet & (\mathscr{C}) \text{ coupe la droite }(\Delta)\text{ au point } A\left(1;2\right) \\ \bullet & (\mathscr{C}) \text{ est au-dessus de la droite }(\Delta) \text{ sur l'intervalle }\left]1;+\infty\right[ \end{matrix}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\begin{matrix} \bullet & (\mathscr{C}) \text{ est en dessous de la droite }(\Delta) \text{ sur l'intervalle }\left]0;1\right[ \\ \bullet & (\mathscr{C}) \text{ coupe la droite }(\Delta)\text{ au point } A\left(1;2\right) \\ \bullet & (\mathscr{C}) \text{ est au-dessus de la droite }(\Delta) \text{ sur l'intervalle }\left]1;+\infty\right[ \end{matrix}} )
6)![\forall x\in ]0;+\infty[\text{ : }h(x)=-x^2+1-\ln x](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]0;+\infty[\text{ : }h(x)=-x^2+1-\ln x)
La fonction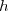 est dérivable sur
est dérivable sur ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) comme somme de fonctions dérivables
comme somme de fonctions dérivables ![]0;+\infty[](https://latex.ilemaths.net/latex-0.tex?]0;+\infty[) .
.
![\begin{matrix}\forall x\in ]0;+\infty[\text{ : } h'(x)&=& \left(-x^2+1-\ln x)\right)'&=& -2x-\dfrac{1}{x} &=& -\dfrac{2x^2+1}{x} \end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix}\forall x\in ]0;+\infty[\text{ : } h'(x)&=& \left(-x^2+1-\ln x)\right)'&=& -2x-\dfrac{1}{x} &=& -\dfrac{2x^2+1}{x} \end{matrix})
Or,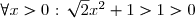 . Donc
. Donc ![\forall x\in ]0;+\infty[\text{ : }h'(x)<0](https://latex.ilemaths.net/latex-0.tex?\forall x\in ]0;+\infty[\text{ : }h'(x)<0)
Donc:![\boxed{\text{ La fonction }h\text{ est strictement décroissante sur }]0;+\infty[ }](https://latex.ilemaths.net/latex-0.tex?\boxed{\text{ La fonction }h\text{ est strictement décroissante sur }]0;+\infty[ })
Or:
= \lim_{x\to 0^+} -x^2+1-\ln x = 0+1-(-\infty)=+\infty)
= \lim_{x\to +\infty} -x^2+1-\ln x = -(+\infty)+1-(+\infty)=-\infty)
Et puisque=0) , on dresse le tableau de variations de la fonction
, on dresse le tableau de variations de la fonction 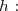
 & \dbarre & & - & & \\ \hline & +\infty&&&& \\ h & \dbarre & \searrow & & & \\ &\dbarre & &0&& \\ &\dbarre & &&\searrow & \\ &\dbarre & && &-\infty \\ \hline \end{array}} )
On en déduit que:
![\boxed{\begin{cases} \forall x\in ]0;1[\text{ : }h(x)>0 \\ h(1) = 0 \\ \forall x\in ]1;+\infty[\text{ : }0 > h(x) \end{cases}}](https://latex.ilemaths.net/latex-0.tex?\boxed{\begin{cases} \forall x\in ]0;1[\text{ : }h(x)>0 \\ h(1) = 0 \\ \forall x\in ]1;+\infty[\text{ : }0 > h(x) \end{cases}})
7) L'équation de la tangente) à la courbe
à la courbe ) au point
au point \text{ s'écrit :})
\text{ : }y=f'(1)(x-1)+f(1) )
Or,=2 \enskip\text{ et }\enskip f'(1)=\dfrac{g(1)}{1^2}=g(1)=1+1-\ln 1 = 2)
Donc:
\text{ : }y=f'(1)(x-1)+f(1)\iff (T)\text{ : }y=2(x-1)+2 \iff \boxed{(T)\text{ : }y=2x })
8) Voir le graphique de la partie B
Partie B:
1) Le graphique:
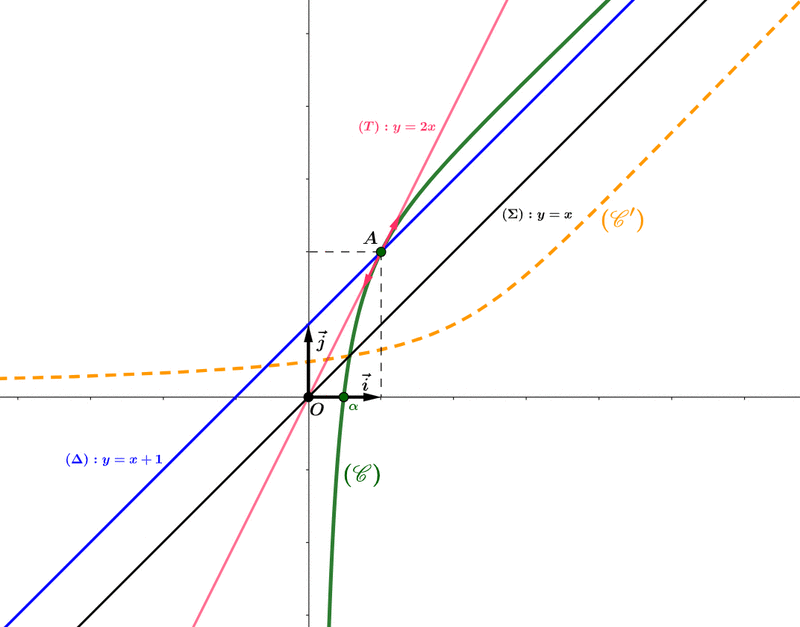
Justification: Puisque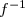 est la bijection récproque de
est la bijection récproque de 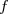 , alors
, alors ) est le symétrique de
est le symétrique de ) par rapport à la droite
par rapport à la droite \text{ : }y=x) .
.
2-a) Soit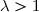 .
.
L'aire) de la partie du plan comprise entre
de la partie du plan comprise entre \text{ , }(\Delta)) et les droites d'équations
et les droites d'équations 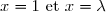 . est en unité d'aire
. est en unité d'aire \text{ : })
=\displaystyle \int_{1}^{\lambda}|f(x)-y|\text{ d}x\enskip \text{avec }y=x+1)
Or , on sait que-y \geq 0 \text{ pour tout réel }x\geq 1 \text{ , alors : } A(\lambda)=\displaystyle \int_{1}^{\lambda}f(x)-y\text{ d}x)
Calculons cette intégrale :
![\begin{matrix} A(\lambda)&=&\displaystyle \int_{1}^{\lambda}f(x)-y\text{ d}x\\&=&\displaystyle \int_{1}^{\lambda}x+1+\dfrac{\ln x}{x}-(x+1)\text{ d}x\\&=&\displaystyle \int_{1}^{\lambda}\dfrac{\ln x}{x}\text{ d}x\\&=& \displaystyle \int_{1}^{\lambda}\dfrac{1}{x}\times \ln x \text{ d}x \\&=& \displaystyle \int_{1}^{\lambda}(\ln x)' \ln x \text{ d}x \\&=& \displaystyle \dfrac{1}{2}\int_{1}^{\lambda} 2(\ln x)' \ln x \text{ d}x\\&=& \dfrac 1 2\left[(\ln x)^2\right]_{1}^{\lambda}\\&=& \dfrac 1 2 \left((\ln \lambda ) ^2 -(\ln 1)^2 \right) \\&=& \dfrac{1}{2} (\ln \lambda )^2 \enskip (U.A.)\end{matrix}](https://latex.ilemaths.net/latex-0.tex?\begin{matrix} A(\lambda)&=&\displaystyle \int_{1}^{\lambda}f(x)-y\text{ d}x\\&=&\displaystyle \int_{1}^{\lambda}x+1+\dfrac{\ln x}{x}-(x+1)\text{ d}x\\&=&\displaystyle \int_{1}^{\lambda}\dfrac{\ln x}{x}\text{ d}x\\&=& \displaystyle \int_{1}^{\lambda}\dfrac{1}{x}\times \ln x \text{ d}x \\&=& \displaystyle \int_{1}^{\lambda}(\ln x)' \ln x \text{ d}x \\&=& \displaystyle \dfrac{1}{2}\int_{1}^{\lambda} 2(\ln x)' \ln x \text{ d}x\\&=& \dfrac 1 2\left[(\ln x)^2\right]_{1}^{\lambda}\\&=& \dfrac 1 2 \left((\ln \lambda ) ^2 -(\ln 1)^2 \right) \\&=& \dfrac{1}{2} (\ln \lambda )^2 \enskip (U.A.)\end{matrix})
Finalement, l'unité graphique est = 4\text{ cm}^2)
Donc:=\dfrac{1}{2}(\ln \lambda)^2\enskip (U.A)=4\times \dfrac{1}{2}(\ln \lambda)^2\enskip (\text{ cm}^2) \enskip \Longrightarrow \enskip \boxed{A(\lambda)=2(\ln \lambda)^2\enskip (\text{ cm}^2)})
b) Puisque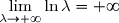 , alors
, alors ^2=+\infty)
Et donc :=+\infty})
Partie C:
\text{ : }\begin{cases} x(t)=e^t \\ y(t)=1+e^t+te^{-t} \end{cases}\text{ ; }t\in \R)
1) On a, pour tout=e^t>0 \text{ , donc }t=\ln (x(t)))
Donc:=1+e^t+te^{-t}=1+x(t)+\ln(x(t)) e^{-\ln(x(t))} = 1+x(t)+\ln(x(t))\times \dfrac{1}{x(t)})
On en déduit l'équation cartésienne de) est :
est :
=1+x+\dfrac{\ln x}{x}=f(x) })
Remarque:) n'est autre que la courbe
n'est autre que la courbe ) .
.
2) Notons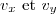 les coordonnées du vecteur vitesse
les coordonnées du vecteur vitesse 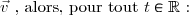
=\dfrac{d x(t)}{d t} = (e^t)' =e^t)
&=&\dfrac{d y(t)}{d t} &=& (1+e^t+te^{-t})' & =&e^t+e^{-t}-te^{-t}& = &e^t+(1-t)e^{-t} \end{matrix})
Pour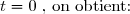
=e^{0}=1)
=e^0+(1-0)e^0=1+1=2)
Conclusion:
})
Bac Mathématiques
Burkina Faso 2023
Série F1-F2-F3-F4
1er tour
Coefficient: 5
Calculatrice non autorisée
4 points
exercice 1

4 points
exercice 2

12 points
probleme


exercice 1
A)
1) On a pour tout
Donc:
Montrons que
On a:
Donc:
2) On a, pour tout
Donc:
On en déduit que:
3-a) La suite
D'où:
b) On a:
On obtient:
De plus:
On en tire que:
c) Puisque
B)
1) On a
Donc:
2) Calculons
exercice 2
1) Soit
Donc:
2) L'équation différentielle
Donc les solutions de
L'ensemble des solutions de
3) Soit
4) Soit
On en tire que:
L'ensemble des solutions de
5)
Il s'ensuit:
probleme
Partie A:
1) La fonction
Étude de signe:
On sait que:
Or,
Dressons le tableau de signe:
On conclut alors que:
2) Calculons
Ayant étudié le signe de
On en tire que
Donc:
Finalement:
D'où:
3)
Calcul des limites:
Interprétation graphique:
4-a) La fonction
Vérification:
b) D'après ce qui précède, la fonction
De plus,
On obtient alors:
Et on dresse le tableau de variations de la fonction
c) La fonction
De plus,
Et puisque
On en tire que
Encadrement de
On en déduit que :
Et en sachant que
5) Soit
Interprétation graphique:
Étude de la position relative:
Étudions le signe de
Et puisque:
Finalement, si
On en déduit que:
6)
La fonction
Or,
Donc:
Or:
Et puisque
On en déduit que:
7) L'équation de la tangente
Or,
Donc:
8) Voir le graphique de la partie B
Partie B:
1) Le graphique:
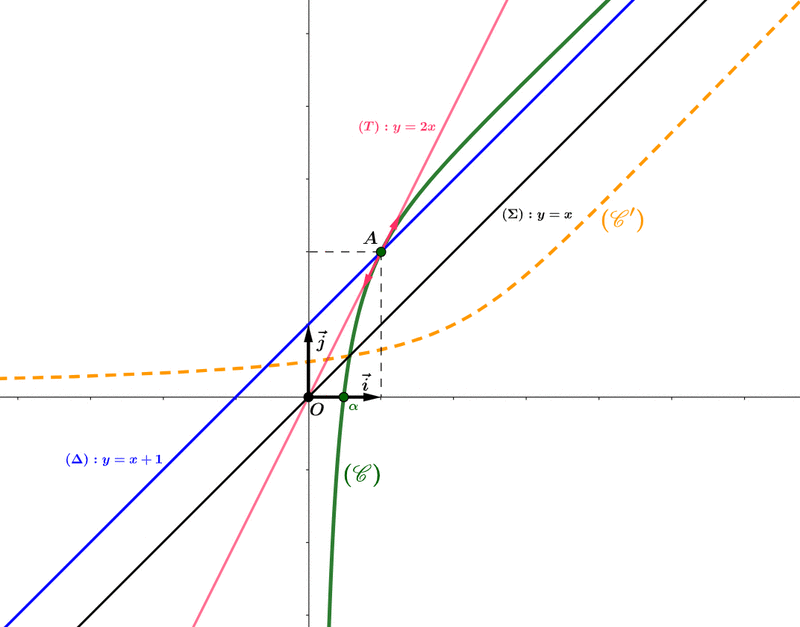
Justification: Puisque
2-a) Soit
L'aire
Or , on sait que
Calculons cette intégrale :
Finalement, l'unité graphique est
Donc:
b) Puisque
Et donc :
Partie C:
1) On a, pour tout
Donc:
On en déduit l'équation cartésienne de
Remarque:
2) Notons
Pour
Conclusion:
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter

 Voir la correction
Voir la correction forum de terminale
forum de terminale