Fiche de mathématiques
Ile mathématiques > maths bac > Bac 2023 toujours : des sujets venus d'ailleurs
Bac Tchad 2023
Durée : 4 heures
Coefficient : 5C - 4E
Une urne contient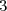
boules noires, 
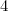boules rouges et 
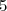boules blanches indiscernables au toucher. On tire successivement et sans remise 
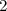boules de l'urne.
1) Calculer la probabilité de tirer:
a) A: «Deux boules rouges»
b) B: «Deux boules de couleurs différentes»
2) On inscrit sur chaque boule noire le numéro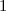
, sur chaque boule rouge 
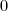et sur chaque boule blanche le nombre 
.
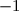On considère la variable aléatoire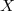
qui, à chaque paire de boules tirées, fait correspondre la somme des chiffres inscrits sur les deux boules.
a) Déterminer la loi de probabilité de.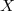
b) Calculer l'espérance mathématique de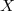, la variance et l'écart-type.
c) Définir et représenter la fonction de répartition de.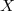
Le plan complexe est muni d'un repère orthonormal direct)
(unité graphique: 
).
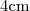Soit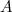
le point d'affixe 
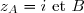le point d'affixe 
.
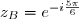1) Soit
la rotation de centre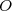 
et d'angle 
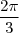. On appelle 
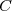l'image de 
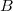par .
a) Déterminer une écriture complexe de .
b) Montrer que l'affixe de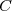 est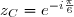 
.
c) Écrire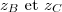
sous forme algébrique.
d) Placer les points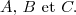
2) Soit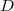
le barycentre des points 
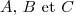affectés respectivement des coefficients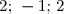 
a) Montrer que l'affixe de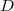 est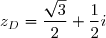 
. Placer le point .
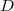b) Montrer que les points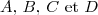
sont situés sur un même cercle.
3) Soit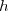
l'homothétie de centre 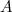et de rapport 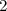. On appelle 
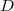l'image de par .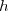
a) Déterminer une écriture complexe de.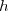
b) Montrer que l'affixe de est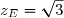 
. Placer le point .
4) a) Calculer le rapport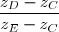
. On écrira le résultat sous forme exponentielle.
b) En déduire la nature du triangle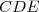
.
On définit la fonction numérique
définie sur 
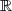par:
=\begin{cases} \dfrac{\ln x}{1+x} &\text{ si } x\geq 1 \\\\ e^{\frac{1}{x-1}}&\text{ si } x< 1\end{cases} )
On note)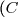
la courbe représentative de dans un plan muni d'un repère orthonormal )
tel que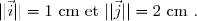 
Partie A
Soit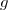
la fonction numérique définie sur 
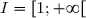par =1+x-x\ln x)
.
1) Calculer les limites de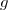 aux bornes de 
.
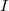2) Étudier le sens de variation de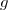 et dresser son tableau de variation.
3) Démontrer que l'équation=0)
admet une unique solution 
sur .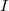
Vérifier que![\alpha \in ]3,5\text{ ; }4[](https://latex.ilemaths.net/latex-0.tex?\alpha \in ]3,5\text{ ; }4[)
.
4) Déduire de ce qui précède le signe de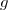 sur .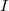
Partie B
1) Calculer les limites de en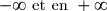 
.
2) Étudier la dérivabilité de en 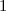. Interpréter graphiquement le résultat obtenu.
3) Calculer)
pour tout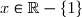 
et vérifier que pour tout =\dfrac{g(x)}{x(1+x)^2})
4) En déduire le signe de pour tout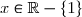 
puis dresser le tableau de variation de .
5) Montrer que=\dfrac{1}{\alpha})
.
6) Construire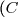 , ses tangentes et ses asymptotes .
Partie C
On pose^n\text{ d}x \text{ pour tout }n\in\N)
.
1) Calculer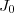
.
2) Montrer que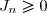
pour tout 
.
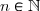3) Montrer que)
est décroissante.
4) Montrer que est convergente.
5) En utilisant une intégration par parties, démontrer que pour tout entier naturelJ_n=e^3)
.
6) En déduire les valeurs exactes de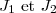
.
Données:\approx 1,25\enskip\text{ ; }\enskip \ln 2 \approx 0,7\enskip\text{ ; }\enskip e^{-1}\approx 0,37)
Publié par malou/Panter
le
Bac Tchad 2023
Mathématiques séries C-E
Coefficient : 5C - 4E
exercice 1
Une urne contient
1) Calculer la probabilité de tirer:
a) A: «Deux boules rouges»
b) B: «Deux boules de couleurs différentes»
2) On inscrit sur chaque boule noire le numéro
On considère la variable aléatoire
a) Déterminer la loi de probabilité de
b) Calculer l'espérance mathématique de
c) Définir et représenter la fonction de répartition de
exercice 2
Le plan complexe est muni d'un repère orthonormal direct
Soit
1) Soit
a) Déterminer une écriture complexe de
b) Montrer que l'affixe de
c) Écrire
d) Placer les points
2) Soit
a) Montrer que l'affixe de
b) Montrer que les points
3) Soit
a) Déterminer une écriture complexe de
b) Montrer que l'affixe de
4) a) Calculer le rapport
b) En déduire la nature du triangle
probleme
On définit la fonction numérique
On note
Partie A
Soit
1) Calculer les limites de
2) Étudier le sens de variation de
3) Démontrer que l'équation
Vérifier que
4) Déduire de ce qui précède le signe de
Partie B
1) Calculer les limites de
2) Étudier la dérivabilité de
3) Calculer
4) En déduire le signe de
5) Montrer que
6) Construire
Partie C
On pose
1) Calculer
2) Montrer que
3) Montrer que
4) Montrer que
5) En utilisant une intégration par parties, démontrer que pour tout entier naturel
6) En déduire les valeurs exactes de
Données:
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
forum de terminale