Bonsoir,

Effectivement plumemeteore avait résolu ce
problème en "lycée" en 2011 ,mais pour 2
cercles différents on va phosphorer.

oui.

ma dernière phrase souligne la difficulté de la chose.
elle suggère que ce ne serait pas possible à la règle et au compas.
alors comment faire ?

pour clarifier le débat disons qu'on a le droit d'utiliser les instruments géométriques de Geogebra (équivalents de règle et compas + tracé de coniques)
il faudra justifier qu'ils sont indispensables...
(ou l'infirmer en trouvant tout de même une construction règle et compas, je ne suis pas infaillible)

Bonjour,

Je blanke

 Cliquez pour afficher

Comme tu le détestes ,ma première idée est d'aller
chercher ces fameuses décimales...ça c'est fait.
exemple R=12 et r=8 a=3.88911
Je peux calculer en 3 secondes

La formule est:
a=(R+r)²-(R-r)²-r²-(r-a)²-R²-(R-a)²

Pour une solution sangaku ,on attend les ténors

Bonjour,
un ancien comme toi devrait mieux maitriser les parenthèses !!!
comment le reprocher aux élèves ensuite ?

ce que tu donnes n'est pas une formule mais une équation (il y a l'inconnue "a" des deux côtés)
alors certes on peut résoudre cette équation par des méthodes d'approximations successives...
(les formules de Cardan et Ferrari étant inutilisables en pratique, on tombe en fait sur une équation du 4ème degré)

Citation :
Pour une solution sangaku, on attend les ténors

RE

Ce ne sont pas les parenthèses que je ne maitrise pas
mais le toit des

le toit des se traite de la même façon que la longueur des "/" : en ajoutant des parenthèses
ceci dit la cohérence des dimensions (on ne peut pas ajouter un carré de longueur et une longueur) permet au lecteur attentif de deviner où sont les parenthèses manquantes :

 Cliquez pour afficher

a=(R+r)²-(R-r)²-r²-(r-a)²-R²-(R-a)²

c'est à dire

Bonsoir,

 Cliquez pour afficher

Voici j'espère, une construction du carré (conique passant par 5 points)

j'ai exactement la même


(sauf que au lieu de fixer R et r pour construire les deux cercles de départ, j'ai fixé R et ton OH, distance des points de contact avec la droite, mébof, les deux cercles sont "donnés" )

reste à justifier tout ça ...
que c'est une ellipse etc et qu'il n' y a pas de construction sans coniques

Bonjour,

La solution a été trouvée par "amateur", encore bravo

je vais donner quelques développements pour finaliser cet exo

construction géométrique :
tout repose sur une transformation du plan appelée "transvection"
c'est une translation parallèle à l'axe mais dont le module est proportionnel à la distance du point à l'axe
ici le coefficient de proportionnalité est 1 : l'image du point M est le point M' qui complète le carré MM'H'H

tous les points de l'axe sont invariants
l'image d'une droite d est une droite d'
l'image d'une conique est une conique de même nature
la transvection conserve les incidences (droites sécantes et tangentes) les rapports de longueurs et les aires, mais pas les angles
l'image d'un cercle est donc une ellipse et le centre de l'ellipse est l'image du centre du cercle.

pour notre problème ...

 Cliquez pour afficher

l'image de tout point D du cercle de centre O est donc le sommet C d'un carré qui s'appuie sur le cercle (O) en D et sur la droite (UV)
le point C cherché est donc l'intersection de l'ellipse, image du cercle (O) dans cette transvection, avec l'autre cercle (O')
reste à définir précisément cette ellipse pour la tracer de façon continue, et pas point par point.
la règle du jeu (outils géométriques de Geogebra) autorise le tracé d'une ellipse définie par 5 points
il suffit donc de construire 5 points particuliers de l'ellipse pour achever la construction.

les points U U (point fixe sur l'axe), Y U' , W O, Z s'obtiennent instantanément sur une grille de module R
est même le centre de l'ellipse (image de O)
reste donc à contruire un 5ème point au hasard par la transvection
j'ai choisi le point Q "à 45°" dont l'image est construite en P en appliquant la transvection
ce point est intéressant car en ce point la tangente à l'ellipse est verticale
mais n'importe quel point sur le cercle (O) et son image ferait aussi bien l'affaire

on a donc nos 5 points et c'est fini

Construction de l'axe puis des foyers je pense .

c'est assez sibyllin tous ces traits...

les petits malins montreront que les axes ont pour coefficient directeur -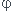 et 1/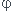 avec apparition inattendue du nombre d'or...

attention : la construction des foyers et axes ayant pour but de permettre le tracé de l'ellipse sans utiliser la fonction "ellipse par 5 points", cette construction ne doit pas faire intervenir du tout le tracé préalable de l'ellipse elle-même !
(sinon ça n'offre aucun intérêt de construire les foyers et axes : On tape sous Geogebra Foyers[c] et terminé !!)

Oui , le schéma était un peu chargé . Je n'ai laissé que la construction de 6 points de l'ellipse (tracés bleu) puis en rouge les axes et les foyers .

Bonjour

Quand je disais les ténors...

Il n'empêche que malgré l'épuration, je n'ai pas entièrement compris cette construction.
(et sans noms de points c'est difficile d'en discuter)

ajoutons les (par rapport à ma propre figure) :


ton principe pour construite les axes est de construire surtout les point A, A', B, B'
A et A' ne présentent aucune difficulté de compréhension, après tout A est le sommet du carré du problème à deux cercles égaux, j'ai même ajouté la construction de caylus (problème d'origine Problème sangaku) de ce point, comme intersection de OX et GU', G milieu de UX.
la suite consiste donc à construire les points B et B' comme intersections de XY avec le cercle de centre passant par A
pourquoi ces points sont-ils sur l'ellipse ???

si oui (= une fois justifié) la construction des axes comme bissectrices de AB est directe.

B est en fait l'image de C dans la transvection, mais vu ainsi la preuve n'est pas plus visible :
si B est construit comme intersection de XY (image de XW) par la parallèle à (UX) passant par C, (donc sur l'ellipse par construction) il faudrait prouver qu'il est sur le cercle (que A = B) ??

ma construction des axes est bien plus simple, mais fait intervenir "quelques calculs préalables" (quelques lignes) pour prouver que leurs coefficients directeurs sont -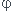 et 1/)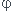

ensuite ta construction des foyers est tout aussi mystérieuse ...
(la mienne est plus compliquée mais ne fait intervenir que des propriétés élémentaires de l'ellipse)

A'  est à l'intersection des droites  d(x) = 2x + 1    et   d'(x) = -x/2 + 1/2   . Son abscisse est pour x tel que   2x + 1 = -x/2 + 1/2     soit   2x + x/2 = -1/2    5x/2 = -1/2   et  

x(A') = -1/5  
y(A') = -2/5 + 1 = 3/5

Le cercle de rayon OA'  a pour rayon  r = sqrt ((1/5)² + 3/5)²) = sqrt ((1+9) / 5²) = sqrt(10) / 5
L'équation de ce cercle est donc  x² + y² = r² = 10 / 25  soit   y = sqrt (10/25 - x²)
L'intersection de la droite d"(x) = -x  avec ce cercle donne   -x = sqrt (10/25 - x²)  et  x² = 10/25 - x²
Soit  2 x² = 10/25    et   x  = ± sqrt(5) / 5

x(B') = - sqrt(5) / 5
y(B') =   sqrt(5) / 5

La droite  A'B'   a pour équation   y = ax + b
En A'    3/5  = -a/5 + b
En B'    sqrt(5) / 5 = -sqrt(5) a / 5  + b
-------------------------------------------------  la différence entre ces 2 équations donne  :
3/5 - sqrt(5) / 5 =  a (sqrt(5)/5 - 1/5 )    et  a  = (3-sqrt(5)) / (sqrt(5) -1)

1/a = (sqrt(5) -1) / (3-sqrt(5))  =  (sqrt(5) -1) (3+sqrt(5)) / (3-sqrt(5)) (3+sqrt(5))
1/a = (3 sqrt(5) + 5 - 3  - sqrt(5)) / 9 - 5   =   (2 sqrt(5) + 2) / 4  =  (1 + sqrt(5)) / 2
1/a = φ

calcul intéressant mais qui ne justifie toujours pas que B' est sur l'ellipse !!
le problème est là
je ne dis pas que ta construction n'est pas bonne, j'en demande seulement la preuve
à part de façon totalement calculatoire (en remplaçant tes coordonnées de B' dans l'équation de l'ellipse, totalement beurk)

Bon alors comme la construction de fm_31 est toujours incompréhensible (= non justifiée)
je donne la mienne (les miennes)

tout d'abord les axes.
ma construction rapide est celle qui utilise un calcul algébrique préalable

dans le repère d'origine U et d'abscisses (UV) le cercle (O) a pour équation x² + (y-R)² = R²
la transvection opère la transformation x -> x + y, y -> y
l'équation de l'ellipse est donc (x-y)² + (y-R)² = R² dont les termes de plus haut degré sont x² - 2xy + 2y²
les vecteurs propres de la matrice associée sont et

ce qui définit les axes de l'ellipse :
les coefficients directeurs des axes de l'ellipse sont donc et

d'où la construction rapide de ces axes :

le cercle de centre I milieu de OY et passant par coupe (OY) en E et E'
les axes sont les droites E et E'
construction classique du nombre d'or

Une construction sans calcul préalable utilise la définition suivante des axes d'une conique : paire de diamètres conjugués orthogonaux, mais c'est plus compliqué.

on construit donc deux paires de diamètres conjugués

UU' et OZ conjugués (facile car la propriété que les tangentes aux extrémité de l'un sont parallèles à l'autre est triviale ici)
et
AA' conjugué de PP'
la tangente en P est verticale (la construction de P a été choisie pour, déja discuté)
il est un tout petit peu moins visible de justifier que AA' est vertical

ce qui définit une involution (la conjugaison des diamètres) sur le faisceau de droites *
on projette ce faisceau sur un cercle passant par , ça tombe bien on en a déja un.
(seconde intersection des droites de * avec le cercle)

l'involution sur ce cercle est ainsi définie par deux paires de points conjugués
W U et B

le centre de cette involution est construit comme intersection de UW et de B
enfin on trace le diamètre IJ du cercle passant par
les axes sont les projections inverses de I et J sur le faisceau *, c'est à dire I et J

pour ne pas surcharger ce message je ne montre pas ma construction des foyers...

Oui effectivement il manquait une preuve .
En démontrant que A = B , on démontre que A et B sont bien sur le même cercle de rayon  √2 / √5 .

AD = 2/5 = HG    et   AH = 1/5     (R=1)
ΩH = 1 - 2/5 = 3/5
AΩ² = (3/5)² + (1/5)² = 10/25 = 2/5

CL = CB  
sin θ = 1 / √5 = CL / (√5 - 1)
CL = BM =  (√5 - 1) / √5
XB = BM √2 = √2 (√5 - 1) / √5
BΩ = ΩX - XB = √2 - (√2 (√5 - 1) / √5)
       = (√2√5 - √2√5 + √2)) / √5
       = √2 / √5 = AΩ

C'est bien mieux ... mais c'est trop calculatoire à mon goût

pour compléter avec ma construction (toujours dans le style expéditif) des foyers
on utilise la propriété élémentaire que la tangente et la normale à l'ellipse sont les bissectrices des rayons vecteurs :

si on considère le cercle circonscrit à FF'A et les bissectrices de l'angle A on retrouve la propriété élémentaire classique que les intersections des bissectrices avec ce cercle sont sur la médiatrice de FF'

et donc inversement la construction des foyers :
la tangente et la normale coupent l'axe transverse en D et E
le cercle de diamètre DE coupe l'axe focal en les foyers cherchés (plus rapide que les intersections I et J des tangentes et normales avec l'axe focal et construction de la division harmonique (F, F', I, J))

ce qui donne sur notre figure la construction complète des axes et foyers :

on est d'accord mais j'aime moins.

surtout que niveau 3ème il manque vraiment trop de trucs dans le programme (triangles semblables par exemple, nécessitant de passer par une expression explicite via des fonctions trigo réellement inutiles, etc) pour que les calculs ne deviennent pas très vite "filandreux".
en plus ici c'était même Thalès CL/R = XC/XO
nota : il faut ajouter ici le calcul de l'exo de collège d'origine (deux cercles égaux) pour affirmer que le côté du carré AD = 2/5

Ce qui m'a le plus intéressé dans cette ellipse c'est l'apparition de phi . C'est pas très courant à ma connaissance . Merci donc pour cette détente .