Inscription / Connexion Nouveau Sujet
ABCD un parallélogramme
bonjour a tous pouvez vous m'aider ? 
ABCD un parallelogramme et e f g et h les milieux respectifs des cotes AB BC CD ET DA la diagonale BD coupe les segments AF et AG respectivement en M et N
a determiner les coordonnées des points a b c d e f g et h les le repere (A;AB;AC ) ( vecteurs )
voici ma reponse A(0;0) B(1;0) C(0;1) E(1/2;0) apres je n'y arrive pas ! 
b determiner les equations des droites (AF) (AG) et (BD)
c en deduire les coordonnées des points M et N
d montrer que DN= NM = MB ( vecteurs )
e demontrer que les points E, M et C sont alignés
f demontrer que les points H, N et C sont alignés
voici ma figure desolé pour la qualité
Bonjour,
effectivement l'image est 
en voila une plus lisible
coordonnées de A(0;0) B(1;0) C (1;1) D(0;1) E(1/2;0) F(1;1/2) G(1/1;1) H(0;1/2)
tu peux continuer maintenant...
merci pour ton schema et ta reponse !!
mais je crois que tu as faux s'en vouloirs te fexé
mais pour les coordonées des points on se place dans le repere (A;AB;AC) ( vecteurs )
C ne fait pas 1 fois le vecteur AB mais 0 et une foi le vecteur AC donc C(0;1) et D ( -1;1 )
( G(1/2;1) H je ne sais pas ) pour ces deux points la je ne suis pas sur...
non tu ne me vexespas...il m'arrive de me tromper et c'est ce que j'ai fait en prenant le repère (A; AB ; AD) ce qui me paraissait plus évident.....
Je rectifie en essayant de ne pas me tromper :
A(0;0) B(1;0) C(0;1)
E(1/2;0)
D(-1;1)
F(1/2;1/2) et H(-1/2;1/2): trace les parallèles aux axes passant par F et par E pour mieux comprendre...
G(-1/2;1)
alors la question B determiner les equations de droite ( AF ) donc je prends
AF : A( 0;0 ) et F ( 0.5 ; 0.5 )
y=ax+b donc 0 = b
0.5= 0.5 + b
b=0
et
0.5-0.5=b
0 = b
j'ai trouver pour ( BD )
b ( 1 ; 0) et d ( -1; 1)
donc y= ax +b
donc 0= 1a+b
1= -1a +b
2b = 1
b= 0.5
1a+0.5=0
1a= -0.5
donc y= -0.5+0.5
pour (AF) :
y = 0,5x
pour (BD) :
y =-0,5x + 0,5
pour (AG) :
b = 0 car la droite passe par l'origiien
donc l'équation est de la forme y = ax
G(-0,5;1) est sur la droite donc 1 = -0,5a et a = -1/0,5 = -2
équation de (AG) :
y = -2x
ah non j'ai trouver AF 0= a *0 +b
0.5= a *0.5 + b
b=0
0.5= a*0.5 +b
0.5=a*0.5 + 0
y= x
et pour BD il manque un x donc c'est y= -0.5x+0.5
et voici peut etre la solution pour AG A( 0;0) G(-0.5;1)
0=b
1= -0.5x + b
1= -0.5x+0
0.5x=-1
x=-1/0.5 = -2
donc y = -2x
ah tu as envoyé le message avant moi on n'arrive a la question C
c'est en fonction des vecteurs ? pourrait tu me donné le debut... pour que j'essaye de finir !
??????????????? ok
alors pour la c en deduire les coordonnées des points M et N alors il faut se servir des responses precdentes
le point N est sur la droite AG et M est sur la droite AF
mais comment faire ? prendre le mileu de l'quation de la droite ?
ah cocoque est revenu....
prendre le mileu de l'quation de la droite ?
c'est quoi le milieu de l'équation d'une droite
N est sur la droite (AG) et sur la droite (BD)
équation de (AG) : y = - 2x
équation de (BD) : y = -0,5x + 0,5
résous le système pour avoir les coordonnées de N
non 
ce n'est pas comme cela qu'on résout un système de deux équations à deux inconnues...
la méthode des substitutions, par exemple, ça te dit quelque chose ?
oui
alors pour le point N
y=-2x
y=-0.5x+0.5
je passe les calculs..
j'arrive a x=-1/3
et y=2/3
le point M je prend l'equation de la droite AF et BD
y=0.5x
y=-0.5x+0.5
je passe les calculs aussi..
j'arrive a x=0.5
et y=0.5 x 0.5
y=1/4 soit 0.25
alors D(-1;1) N(-1/3 ; 2/3 ) M(0.5;0.25) B(1;0)
vecteur DN = (2/3 -1/3 ) NM ( 5/6 -5/12 ) et MB ( 0.5 -0.25 )
je fais la colinearité et je trouve -5/18-(-5/18)=0 donc ils sont alignés... c'est bon ?
donc alors se que j'ai compris
il faut que je fais la " formule " suivante:
xy' et x'y
pour DN NM et MB
DN (2/3 -1/3 ) et NM ( 5/6 -5/12 ) et MB ( 0.5 -0.25 )
pour DN et NM 2/3 * ( -5/12 ) =-5/18
et -1/3 * 5/6 = -5/18 donc ils sont colineaires et donc alignés....
si c'est la bonne reponse je dois continuer avec NM et MB
je veux montrer que DN=NM=MB ( vecteurs )
donc j'utilise la colinearité...si par exemple le vecteur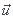 
= 2 *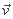 
donxc ils sont alignés... non ?
je t'ai écris à 12 :18, mais tu n'as pas lu semble-t-il
tu dois démontrer que les vecteurs sont égaux cela signifie qu'ils ont les mêmes coordonnées
pour démontrer que des vecteurs sont égaux il faut prouver qu'ils ont les mêmes coordonnées
regarde mon dernier post, je te signale une erreure, recalcule d'abord les coordonnées de M
ensuite tu recalculeras les coordonnées des trois vecteurs et tu devrais consytater que ce sont les mêmes...
oui alors af = y=x
donc pour M je passe les calculs x = 1/3 et y = 1/3
pour le vecteur DN = ( 2/3 ; -1/3 )
pour le vecteur NM = ( 2/3 ; -1/3 )
et MB le meme donc DN=NM=MB
question E maintenant je ne sais comment faire...
voila ...c'est bon maintenant
questions e et f)
e demontrer que les points E, M et C sont alignés
f demontrer que les points H, N et C sont alignés
pour démontrer que E, M et C sont alignés, démontre, par exemple, que les vecteurs
Annuler
connectez vous