Inscription / Connexion Nouveau Sujet
Centre de masse d'un cône .
Bonjour ,
Nous ne somme pas sur l'île de la physique , mais je pense que ce problème peut se trouver ici également .
Soit un cône coucher sur son bord de hauteur H et de rayon R déterminer son centre de masse .
Je trouve un centre de masse de 3/4 de la hauteur , est-ce juste ?
Avec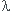 
Densité volumique de masse et en utilisant la formule suivante
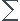Mi.Ri/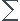Mi=X(centre de masse)
En considérant le cône comme étant décrit sur la figure ci-jointe .
Bonjour ,
tel que représenté , la base verte est une ellipse et R est alors le grand diamètre de l'ellipse mais pas le rayon du cône .
Cordialement
Le schéma ci-dessus est fallacieux : il laisse penser que le centre de masse du cône coïncide avec le centre de gravité du triangle section médiane du cône.
fm_31, es-tu d'accord que c'est faux ?
Je trouve un centre de masse de 3/4 de la hauteur , est-ce juste ?
Oui c'est juste.
Au numérateur tu intègres chaque disque en X² pondéré par X.
Au dénominateur tu intègres simplement chaque disque en X².
Au final tu as X^4/4 divisé par X^3/3 qui donne 3/4.
Ce qui me pose problème dans mon schémas , chose qui est corrigée dans le deuxième schémas , c'est que je considère la "corde latérale" de mon cône (je ne sais pas comment l'appeler autrement) comme étant égale à la hauteur.
Si je pose le problème en faisant l'hypothèse d'un côned'angle d(théta) (représenter en vert sur le deuxième schémas) infinitésimal, du point de vu de la physique je pense que cela pourrait être correct ?
Merci pour la représentation du schémas proprement .
Pourrais tu expliquer une méthode pour trouver ce centre de masse en prenant compte de ton angle (théta) , brièvement ?
Je ne vois pas en quoi le fait que le cône soit couché sur son bord intervient dans le calcul de son centre de masse...
Ce qui importe c'est qu'il soit plein.
Le calcul proposé par fm_31 me semble hors sujet...
Ou alors l'énoncé est équivoque...
C'est vraiment n'importe quoi ce calcul ! fm_31, tu devrais réviser la façon dont on calcule le centre de masse, par exemple ici : 
à défaut de mieux.
Comme l'avait calculé MiSami, le centre de masse est situé sur l'axe du cône, aux 3/4 de la hauteur à partir du sommet. Si le cône est couché sur un plan horizontal, la distance du sommet au projeté du centre de masse sur ce plan est donc
Robot , merci pour le rajout du cos(théta) , je me posais la question car dans mon esprit c'était une approximation que l'ont fesait , or qu'il suffit d'exprimer SA en fonction de la hauteur (connue) et du cos de l'angle , merci .
Prenons un cône d'angle (théta) valant 20 degré par exemple , et de hauteur 20 cm
le centre de masse se trouverait donc à environ 14cm en rajoutant le cosinus , et 15cm sans celui-ci .
L'écart est non négligeable .
La formule de fm_31 donne 14,9 cm , qui n'est donc pas "fausse" car se trouve dans l'écart donné.
Merci
La formule de fm_31 donne 14,9 cm , qui n'est donc pas "fausse"
La formule n'est pas fausse mais ne correspond pas du tout au centre de masse . J'ai mis un certain temps à m'en apercevoir .
Robot , merci pour le rajout du cos(théta) , je me posais la question car dans mon esprit c'était une approximation que l'ont fesait , or qu'il suffit d'exprimer SA en fonction de la hauteur (connue) et du cos de l'angle , merci .
Prenons un cône d'angle (théta) valant 20 degré par exemple , et de hauteur 20 cm
le centre de masse se trouverait donc à environ 14cm en rajoutant le cosinus , et 15cm sans celui-ci .
L'écart est non négligeable .
La formule de fm_31 donne 14,9 cm , qui n'est donc pas "fausse" car se trouve dans l'écart donné.
Merci
@MiSami,
Si ce que tu cherches c'est le centre de masse, il est au trois quart de la hauteur d'un cône plein, que celui ci soit couché sur son bord, en équilibre sur sa pointe ou plongé dans un bocal à poissons...
Donc theta n'intervient pas dans la détermination du centre de masse.
Peut-être intervient-il, si tu cherches par exemple la projection au sol de ce centre de masse... mais ça tu ne l'as dit nulle part. Donc sois prudent dans ce que tu vas faire de ce résultat parce que soit tu n'as pas compris, soit tu as mal explicité ce que tu cherches...
Ok j'ai de nouveau voulu aller trop vite dans mes conclusions , je n'ai pas lu que ce que tu calculais étais la projection sur l'axe x du centre de masse .
je pensais que ce que fm_31 calculais étais également le centre de masse , d'une autre manière .
Ok j'ai de nouveau voulu aller trop vite dans mes conclusions , je n'ai pas lu que ce que tu calculais étais la projection sur l'axe x du centre de masse
Personnellement je n'ai rien fait de tel : je ne t'ai montré aucun calcul.
Je t'ai juste confirmé le résultat que tu as toi même annoncé sans en être certain, à savoir que le centre de masse d'un cône plein se situe au 3/4 de sa hauteur (en partant du sommet).
Et je t'ai donné une explication simplifiée sur le calcul qui conduit à ce résultat (une intégrale en x au cube au numérateur, divisée par une intégrale en x au carré au dénominateur, qui fournit un rapport 1/4 sur 1/3 qui aboutit bien à 3/4).
je pensais que ce que fm_31 calculais étais également le centre de masse , d'une autre manière
Il s'est trompé une première fois en assimilant le centre de masse d'un cône plein (aux 3/4 de h), avec celui d'un triangle (au 2/3 de h) : ce qui est une erreur.
Il s'est ensuite un peu perdu dans la confusion que tu as toi même introduite en parlant de "cône couché sur son bord"... qui est une indication inutile pour le strict calcul du centre de masse.
Je crois que l'histoire de la projection est anecdotique. fm_31 s'est surtout planté en pensant que le centre de masse se situe sur l'axe du cône, à une hauteur qui divise le cône en deux volumes égaux (d'où son ) - ce qui est faux bien sûr.
Je crois que l'histoire de la projection est anecdotique.
fm_31 s'est surtout planté en pensant que le centre de masse se situe sur l'axe du cône, à une hauteur qui divise le cône en deux volumes égaux (d'où son
...Je reconnais avoir fait au moins 3 erreurs sur cet exercice dont une de calcul et 2 sur la méthode de calcul .
En résumé tout faux pour moi . Ca arrive ...
Comme dit Rolland Courbis :
"Il vaut mieux prendre une bonne branlée sur un seul match et gagner les autres... que tous les perdre par un score étriqué !".
Sauf que je n'ai jamais considéré ma participation comme un match où il y aurait quelque chose à gagner .
Et comme mes erreurs ont été vite pointées , j'espère qu'elles n'ont pas trop perturbé MiSami .
Sauf que je n'ai jamais considéré ma participation comme un match
C'était une "image"
.
... où il y aurait quelque chose à gagner...
On a tous quelque chose à gagner en participant ici.
On a tous quelque chose à gagner en participant ici.
Ca c'est vrai : j'ai appris à ne pas confondre centre de masse avec je ne sais plus quoi ...
Mais il vaudrait mieux avoir des nouvelles de MiSami
Merci pour l'éclaircissement de la situation,je pense que c'est ok à présent.
Pêut-être confond tu avec le barycentre ?
Pour la petite information : c'était un exercice posé lors d'un examen , le fait du "cône couché sur son bord" qui est en fait une information pour induire en erreur.
Excusez moi pour mes fautes de compréhension qui ont pas mal induit en erreur également.
Je tien à remarquer aussi l'exactitude des propos de Robot qui nous à permis de cloturer le problème.
Je tiens à remarquer aussi l'exactitude des propos de Robot qui nous à permis de clôturer le problème.
.
Mais TON problème sera réellement "clôturé"...
... lorsque TU auras compris POURQUOI le centre de masse (aussi appelé barycentre) est situé au 3/4 de la hauteur.
Annuler
connectez vous
géométrie en Bts