Bonjour,

Tu dérives par rapport à r, donc r₀ et a sont considérés comme constantes.
Tu as 2 formules à appliquer pour parvenir facilement à ton résultat.
(uⁿ)' = n*u'*u^n-1
(e^u)' = u'*e^u

Montre tes calculs, et si tu n'y parviens pas, je te mettrai le détail.

Bonjour, merci de venir m'aider

(e^u)' = u'*e^u explique le 2 (multiplié par U à la deuxième ligne) mais malgré ces formules j'ai encore du mal.. Peux tu me montrer les détails ?  j'aimerais vraiment comprendre

Je pense que tu peux te dispenser du LaTeX aussi ^^

Je m'en serai dispensé dans tous les cas puisque je ne le maîtrise pas
Alors, on commence par appliquer : (uⁿ)' = n * u' * u^n-1, tout en sachant qu'on dérive par rapport à r comme précisé ci dessus, et en posant u = 1 - e^{- (r - r₀)/a}

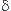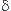/r (1 - e^{- (r - r₀)/a})² = 2 * u' * ( 1 - e^{- (r - r₀)/a} )

u' = ( 1 - e^{- (r - r₀)/a} ) ' . Ici on utilise (e^b)' = b' * e^b avec b = (r - r₀)/a
On a donc u' = 1/a * e^{- (r - r₀)/a} : le (1/a) vient du fait que 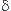/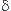r (r - r₀)/a = (1/a) * (r-r₀)'

Mis bout à bout, on obtient ton résultat

Il n'y a que le calcul de u' que je ne comprends pas.

et avec

Pourquoi il n'y a que 1/a qui sort ? On ne calcule pas  (r-r0)' ?

Etant donnée que c'est une dérivée par rapport à r et uniquement par rapport à celui ci, r₀ et a, sont considérés comme constantes.
Pour te simplifier, si tu poses a = une constante, (r)' = , ok jusque là ?
Donc si l'on ne prend que 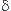/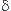r (r-r₀) / a, on obtient donc 1/a car :

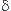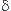/r (r-r₀) / a
= 1/a 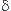/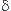r (r-r₀)
= 1/a car r' = 1 et r₀= 0 car constante comme expliqué à maintes reprises

(r₀)' = 0 pardon.

Je croyais que dans les dérivées partielles on conservait les constantes !

Tu écris qui signifie dérivée partielle

alors que dans mon premier message j'ai écrit "d"

Tu conserves les constantes par exemple quand tu as un produit, du style 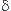/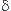r r*r₀ = r₀ mais pour r-r₀ non pas du tout.
Ensuite, oui effectivement, là j'ai parlé de dérivée partielle, parce que ton premier message faisait apparaitre du r₀ et un "a" et que tu n'as rien précisé dessus, mais comme j'ai dérivé toujours par rapport à "r" ( ton " d r " à toi ), il n'y a aucun problème, simplement, peut être, de notation, pour les plus pointilleux d'entre nous