- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Equation paramétrique valeurs absolues
Bonjour,
Il m'est demandé de déterminer les valeurs du paramètre afin que l'équation suivante admette 4 solutions:
Si j'avais eu par exemple:
Je devrais m'en sortir car il suffit que et
Puisque |f(x)|=|g(x)| ssi f(x)=g(x) et f(x)=-g(x)
Mais ce me gêne pas mal...
J'ai essayé d'envisager l'expression de l'équation en fonction des valeurs de x (de -infini à -1, -1 à 1, 1 à 4 et 4 à +infini.
Un exemple avec , j'ai
2 solutions si
J'obtiens et
Sauf que ...
Donc encore trouver les valeurs de $m$ pour que et
...
Il devrait y avoir un autre moyen plus simple. Auriez-vous d'autres idées SVP?
Merci d'avance et bonne journée à vous!
Bonjour,
Il m'est demandé de
Est-ce la première question de l'exercice ?
salut
je ne répète pas les questions de Sylvieg mais une aide tout de même :
le premier membre est positif donc pour avoir des solutions il est nécessaire que le second le soit ...
et même qu'il soit strictement positif si on veut plus de deux solutions ...
ce qui conduit à une conditions sur m ...
Bonjour,
Considérer les deux équations :
x²-1+m(x-4) = 0
x²-1 -m(x-4) = 0
Les deux doivent avoir deux racines distinctes, ce qui impose une condition sur le discriminant de chacune, lesquels discriminants sont des fonctions de m, ce qui impose deux conditions sur m.
Un bilan :
Ehrmantraut n'est pas revenu pour donner un énoncé et son contexte éventuel.
@ LeHibou,
J'ai l'impression que tu ne parles pas de l'équation du 1er message.
@alb12,
J'y ai pensé aussi. J'ai même tenté 1/m = ...
qui est plus simple à priori.
Mais bof.
@carpediem,
Je n'ai pas compris.
Je pensais avoir correctement donné l'énoncé.
L'énoncé est:
"Déterminez toutes les valeurs du paramètre réel non nul de sorte que l'équation
admette 4 solutions.
je laisse traiter le cas m = 0 (sans savoir ce qui se passe à postériori)
le premier membre est positif (par définition d'une valeur absolue)
donc l'égalité ne peut être réalisée (vraie) si le second membre est strictement négatif
posons et
soit le discriminant de ces trinômes est négatif et alors f et g sont positifs
et ... bon trop long à rédiger .... 
je résous l'équation (*) sur les intervalle ]-oo, 4] et [4, +oo[ :
soit dans le premier cas et
dans le deuxième cas
et ... bon trop pénible ... 
tout ce qui précède ne mène à rien (et inachevé) ... sauf à me mener à la solution qui suit 
premier cas : et alors
alors équation du second degré qui ne peut avoir plus de deux solutions
deuxième cas :
alors équation qui ne peut avoir plus de deux solutions à nouveau ...
en espérant ne pas avoir fait d'erreur 
Merci!
Je vais aller regarder à tout ça.
J'ai aussi creusé du côté de et je tombe sur quelque chose de peu convaincant.
Je vais creuser la suite ce soir, je vous tiendrai au courant de l'avancement.
Je sais que c'est un exercice prévu pour prendre 1h.
Pour m non nul, l'équation est équivalente à g(x) = 1/m
avec
.
L'étude du sens de variation de la fonction g sur les intervalles de bornes - , -1, 1, 4 et +
, -1, 1, 4 et + permet de conclure.
permet de conclure.
Pour m = 2024 par exemple, l'équation admet 4 solutions.
@carpediem,
Ta solution n'est pas une solution.
Tu démontres qu'il ne peut pas y avoir plus de 4 solutions.
Pour une même valeur de m, il peut y avoir deux solutions dans chacun de tes deux cas ; ce qui peut donner quatre solutions en tout.
Bonjour,
la résolution séparée dans chacun des intervalles de l'équation d'origine est assez simple si on s'y prend bien
mais il faut obligatoirement s'assurer que les solutions de chacun des intervalles sont dans cet intervalle !
une technique pour savoir si les racines d'une équation du second degré f(x) = ax²+bx+c = 0 sont dans un intervalle I, ici [-1; 1]
totalement inutile d'exprimer explicitement ces racines et d'en déduire des inégalités affreuses
la bonne technique est le signe du trinome :
calculer f(-1) et f(1) et la condition est "du signe de a" (-1 et 1 sont à l'extérieur de [x1 ; x2] )
et l'abscisse du sommet (demi somme des racines) dans l'intervalle
-1 < -b/(2a) < 1
(et bien sur qu'elles existent ...)
Sylvieg : je n'avais pas fini et il faut ensuite bien sûr :
1/ vérifier pour quelles valeurs de m j'ai deux solutions dans le premier cas
2/ faire de même dans le deuxième cas
3/ prendre l'intersection des ensembles précédents

je laisse Ehrmantraut poursuivre ...
Sylvieg
ton équation est g(x) = m
pas 1/m

Et mon 2024 tombe à l'eau...
La nuit porte conseil.
La méthode de carpediem me semble la plus simple.
Après avoir constaté qu'il faut deux solutions dans chacun des deux cas, je conseille de commencer par finaliser le cas x2 -1
 0 .
0 .
En déduire une première condition sur m.
Le second cas que Ehrmantraut a commencé à étudier devient alors un peu plus simple.
Utiliser "la bonne technique" de mathafou :
Exploiter f(-1) et f(1) où f est le polynôme de degré 2.
Et f(0) peut-être.
f(0) est un peu plus compliqué car on pourrait parfaitement avoir
f(-1), f(0) et f(1) du signe de a
indiquant que les racines ne seraient pas entre -1 et 1 alors que si, peut être
il faut affiner
a
Bonjour,
Il semble que la piste de Sylvieg ici :
Pour m non nul, l'équation est équivalente à g(x) = 1/m m
avec
soit abandonnée.
Pourtant elle donne un résultat correct moyennant l'exploitation du nombre de solutions sur chacun des 4 intervalles définis par les valeurs
On peut réduire la discussion en s'y prenant de la bonne manière.
C'est aussi mon avis.
Il faut savoir qu'un tableau des variations dûment justifié suffit pour conclure.
car je ne suis pas sur que calculer la dérivée de (2x²+1)/(4-x) soit vraiment plus simple 
d'autant qu'il faut de toute façon découper ça en 4 morceaux
mais bon, ça fonctionne aussi...
et une fois qu'on a bien étudié les variations cela devient instantané.
Je suis d'accord lake.
Mais privilégier la piste amorcée par le demandeur, en l'occurrence Ehrmantraut, sera sans doute plus satisfaisant pour lui 
Mais privilégier la piste amorcée par le demandeur, en l'occurrence Ehrmantraut, sera sans doute plus satisfaisant pour lui

Là, je m'incline

Et j'attends une bonne conclusion qui pourra satisfaire Ehrmantraut.
>>mathafou
car je ne suis pas sur que calculer la dérivée de (2x²+1)/(4-x) soit vraiment plus simple

d'autant qu'il faut de toute façon découper ça en 4 morceaux
A aucun moment je n'ai eu besoin de dérivées pour conclure.
on peut certes étudier les variations du morceau (2x²-1)/(4-x) autrement
pas sur que ce soit plus simple
(il faut bien en étudier les variations entre -1 et 1 et prouver que son minimum y est < 0)
Bonsoir,
J'essaie d'expliquer mon histoire de f(0) en la remplaçant par le signe du produit des racines.
f(x) = 2x2 + mx - (4m+1)
Tout d'abord, le cas 2), c'est à dire deux solutions extérieures à [-1;1], donne entre autres la condition m > 0.
Dans le cas 1), on veut que l'équation f(x) = 0 admette deux solutions comprises entre -1 et 1.
C'est une équation de degré 2.
Si m > 0, son discriminant est positif ; elle a donc deux solutions distinctes a et b.
De plus ab < 0 ; on a donc a < 0 < b.
On veut -1 < a < 0 < b < 1.
Ce qui revient à f(-1) > 0 et f(1) > 0.
Encore merci à tout ceux qui ont contribué à ce post.
J'en ai discuté avec le professeur qui dispense le cours dont cet exercice est issu et il m'a indiqué que comme évoqué dans le post, le plus simple selon lui c'est que:
(si on veut que )
Et effectivement, c'est plus que logique... J'aurais pu y penser moi-même en traçant la parabole.
De la sorte, les calculs ont été assez rapides et j'en ai conclu que:
1 sol dans si
2 sol dans si
Je terminerai l'exercice plus tard dans la journée et je posterai la réponse finale. Ensuite je me pencherai sur la méthode de Sylvieg qui m'intéresse beaucoup aussi!
je n'ai pas vérifié tes valeurs
mais à priori ici on doit accepter des solutions dans [-1; 1] bornes incluses
pour résumer :
premier cas :
alors
cette équation admet deux solutions
reste à vérifier que les racines appartiennent au bon intervalle ...
deuxième cas :
alors avec
et même
(à cause de la deuxième étape)
or si m > 0 alors évidemment
et
donc deux solutions
attention ensuite aux inégalités pour ne pas trouver -1 ou 1 en solution double ...
Attention :
Dans le second cas, 4-1/m peut être supérieur à 1.
Je répète que traiter le second cas d'abord permet d'aborder le premier cas avec la condition m > 0.
Le signe du discriminant est alors immédiat.
tu te compliques bien la vie pour résoudre l'inéquation 5 < 1/m
sachant qu'un nombre et son inverse ont même signe et que la fonction inverse est décroissante sur les intervalles ]-oo, 0[ et ]0, +oo[ alors
5 < 1/ m si et seulement si m > 0 et m < 1/5 donc 0 < m < 1/5
pour Sylvieg :
or
donc l'équation admet deux solutions dans (et ces deux solutions n'ont pas même signe)
on travaille alors avec cette condition sur m pour le premier cas ...
mais je viens de me rendre compte que j'ai fait une erreur :
premier cas :
alors je ne comprenais pas pourquoi je n'avais pas la même expression que Sylvieg
cette équation admet deux solutions
vu les signes de ces racines la condition sur m trouvée précédemment reste donc
le produit des racines est
la somme des racines est
f(1) = 1 - 3m et f(-1) = 1 - 5m permettent de conclure ...
Pas facile d'argumenter quand on est passager sur son téléphone portable.
Pour le second cas, 4+1/m est toujours solution.
Il suffit que 4-1/m le soit aussi pour avoir 2 solutions.
Merci pour ta remarque carpediem, ça aide à progresser.
En fait pour résoudre ça, j'ai juste à visualiser le graphique la fonction de référence (hyperbole).
Je dois visualiser les valeurs de telles que
C'est immédiat du coup que
Sinon, petite question hors sujet:
Est-il possible d'utiliser ce genre d'otuils LaTeX sur le forum?
\begin{align*}
24xy+36x^{2}+4y^{2}&=4 \cdot (6xy+9x^{2}+y^{2})\\
&=4 \cdot (3x+y)^{2}
\end{align*}\begin{aligned}
24xy+36x^{2}+4y^{2}&=4 \cdot (6xy+9x^{2}+y^{2})\\
&=4 \cdot (3x+y)^{2}
\end{aligned}
donne ceci :
on peut simplement écrire en ligne et dans un tel cas poursuivre tout simplement ainsi :
(et en plus ça évite du scrolling !!)
un tel alignement peut être intéressant dans le développement de somme (double) pour aligner (suivant des colonnes des termes identiques (ou opposés) et montrer des simplifications ...
Bonjour,
Me voici plus à l'aise avec un écran et un clavier d'ordinateur.
@Ehrmantraut,
Je me refuse à commenter tes fichiers solution.
Une des règles de l'île est qu'il faut "taper" ses réponses.
Seuls les tableaux pouvaient échapper à cette règle en apparaissant sous forme d'image insérée dans le message.
@tous, je répète le plan que je préconise :
Démontrer qu'il n'y a pas plus de 2 solutions dans [-1;1].
Idem dans ]- ;-1[
;-1[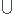 ]1;+
]1;+ [.
[.
On cherche donc pour quelles valeurs de m il y a deux solutions dans chacun des deux cas.
Traiter ]- ;-1[
;-1[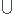 ]1;+
]1;+ [ d'abord.
[ d'abord.
Une première condition nécessaire : m > 0.
Une condition nécessaire et suffisante :
0 < m < 1/5 ou m > 1/3.
Traiter ]- ;-1[
;-1[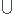 ]1;+
]1;+ [ en sachant que 0 < m < 1/5 ou m > 1/3.
[ en sachant que 0 < m < 1/5 ou m > 1/3.
Conclure.




