Bonjour petite_fee,

Commence par tracer la courbe de la fonction carré.

a) Trace une droite horizontale d'équation y=25 et repère les abscisses correspondants aux intersections avec la courbe. Tu vas pouvoir observer pour quelles valeurs de x on a bien x² inférieur ou égal à 25.

b) Idem en traçant la droite d'équation y=1.

c) Idem en traçant la droite d'équation y=3.

masterrr

Salut, aide-toi de la courbe :

si tout va bien , a) c) n'existe pas

bonjour , c est une simple lecture de la courbe

ahh merci beaucoup
mais je comprend pas quelque chose
donc  
pour x²<25
x appartient à -5 ou 5
c'est bien ça ???

x²>1
x appartient à -1 ou 1

pour x²<3
euh la c'est 3 ou -3 ??

"ladiiie" pourquoi me dis-tu que, je cite "si tout va bien , a) c) n'existe pas" ??

??

pour x²<25
x appartient à -5 ou 5
c'est bien ça ???
oui intervalle fermé  [-5; 5]
b) non ]-;-1[ ]1; +[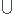
c) ]-1; 1[

pardon c) ]-3 ; +3 [
_{je repondais a plusieurs en meme temps}

ok merci beaucoup !

avec plaisir

Bonjour à tous.
J'ai moi aussi un exercice du même type pour mon devoir maison, je suis en seconde.
Malheureusement,  mon professeur n'a pas donné le cour complet et meme après maintes recherches sur le sujet je suis incapable de faire mon exercice.

Consigne: À l'aide de la courbe représentative de la fonction carré, résoudre chacune des inéquations.
A. x²>2            b. x²≤10
C. 0<x²≤5.     d. 4<x²≤16

Les deux premières inéquations n'ont pas posé de problèmes mais je suis incapable de faire les deux suivantes. J'espère avoir de l'aide d'ici peu, merci à vous.

bonjour

je me demande si tu ne dois pas ouvrir un nouveau topic, étant donné que ce n'est pas exactement le mm énoncé (?)
peut-être un modérateur nous dira.

c)   0<x²≤5
la condition  0< est inutile, car un carré est toujours positif
cela revient donc à résoudre  x²≤5, ce qui ne doit pas te poser difficulté puisque tu as su faire b)

d. 4<x²≤16
cet encadrement est équivalent au système :
{4<x²
{x²≤16

résous ces 2 inéquations séparément, puis détermine l'intersection des ensembles de solutions.
(pour t'aider à ça, tu peux tracer un axe orienté, et hachurer)

Bonjour,

la condition 0< est inutile

pas tout à fait

l'inégalité stricte signifie en fait que x est différent de 0
(ce qui va influer sur l'ouverture ou fermeture des intervalles ou une définition équivalente avec des ensembles : "ensemble E sauf 0")

bonjour Mathafou
... vous avez raison, je suis allée un peu vite, là :s

Merci beaucoup à vous deux, vous m'avez sauvé, vos réponses ont été très utiles !