Inscription / Connexion Nouveau Sujet
Polynômes de Lagrange
Bonjour,
Je n'arrive pas à montrer les égalités suivantes:
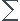 i=0n(xi-x)kLi(j)(x)/j! =
i=0n(xi-x)kLi(j)(x)/j! = 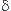 k,j
k,j
Et
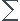 j=0n(xi-x)jLk(j)(x)/j! =
j=0n(xi-x)jLk(j)(x)/j! = 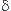 i,k
i,k
Les Li(x) sont les polynômes élémentaires de Lagrange.
Merci pour votre aide.
Bonjour,
La seconde égalité résulte simplement de la formule de Taylor appliquée à .
La première est moins simple.
On peut la démontrer en appliquant la formule du binôme à puis en utilisant la propriété
qui est valable pour tout polynôme de degré (il faut supposer
sinon c'est faux).
Ensuite on dérive j fois , on arrange les factorielles et on obtient le résultat voulu.
On peut démontrer plus simplement la première égalité de la façon suivante.
On applique la propriété au polynôme
(bien distinguer
et
).
On obtient .
Ensuite on dérive fois par rapport à
puis on divise par
.
En distinguant les cas ,
et
on obtient le résultat demandé en remplaçant
par
.


 algèbre en post-bac
algèbre en post-bac