Salut

Ca ce calcul pas avec des fonctions classiques..

Quelle rapidité...

Peux-tu développer ? C'est quoi une fonction classique ? Pourquoi ça ne peut pas se calculer ?

Bonjour

Bien sur, cette fonction continue admet des primitives sur et sur . Seulement on ne peut pas les exprimer avec des fonctions qui ont déjà été repertoriées. Le meilleur exemple est la fonction 1/x qui "n'a pas de primitive" avant que l'on ait introduit le logarithme... Selon leur utilité, on introduit des "fonctions spéciales" quand on a vraiment besoin de travailler avec... A ma connaissance, ce n'est pas le cas pour une primitive de , mais je ne suis pas "spécialiste des spéciales"!

Je n'avais jamais pensé à ça. Mais c'est vrai qu'il y a forcement plein de fonctions qu'on a jamais nommé. C'est aussi le cas de la primitive de e^x², n'est-ce-pas?

Pourtant, il me semble nécessaire de pouvoir exprimer la primitive de e^1/x pour pouvoir résoudre l'équation différentielle

Il ne faut donc pas aller bien loin pour tomber sur de l'inconnu.

Bonjour Michel,

En effet, pour exprimer formellement une primitive de exp(1/x), il faut faire appel à une fonction spéciale.
Camelia a très bien commenté cela.
Les primitives de exp(1/x) s'écrivent formellement par :
x*exp(1/x)+Ei(-1/x)
Le nom de la fonction Ei(X) est "Exponentielle intégrale".
On sait aussi bien la calculer numériquement que les fonctions usuelles sin(x) ou ln(x) ou exp(x), etc.
De même que pour toutes ces fonctions, elle est implémentée dans les logiciels de maths, ce qui permet de programmer les formules où elle figure et de faire les calculs de la même façon que si c'était une fonction usuelle.
Il y a un article de vulgarisation sur les fonctions spéciales à cette adresse :
http://www.scribd.com/people/documents/10794575-jjacquelin
et sélectionner dans la liste : "Safari au pays des fonctions spéciales".

Bonjour JJa, merci on apprend à tout age!

Merci pour votre réponse, et merci aussi pour le lien, votre article est très intéressant.

Donc, ces curieuses choses sont juste méconnues, et ne s'expriment pas à l'aide des seules opérations élémentaires.

Pourtant, sans même parler de l'intérêt purement mathématique, il doit y avoir beaucoup d'applications en physique par exemple, pour ce genre de fonctions. Pourquoi le terme même de "fonction spéciale" est-il méconnu ?

Bonjour,

il ne faut pas croire que le terme "fonction spéciale" soit méconnu. Il apparait seulement à un certain niveau de l'enseignement des mathématiques.
C'est la même chose pour les logarithmes et exponentielles. On commence à les voir à un certain niveau et sont inconnues de ceux qui n'ont pas encore atteint ce niveau.
En dehors du cursus normal, on peut bien évidemment rencontrer ces fonctions et les retrouver dans beaucoup d'ouvrages. En particulier dans les handbooks de maths ou sur des sites comme par exemple http://mathworld.wolfram.com

Bonjour,

Je pense qu'il y a une petite erreur dans le résultat donné par JJa le le 20-05-09 à 17:19.
Une primitive de est et pas .

La définition la plus accessible (au niveau sup) de Ei(x) pour x>0 est:
où 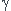est la constante d'Euler.
On en déduit d'où .

Bonjour,

attention de bien faire les distinctions qui s'imposent entre différentes fonctions apparentées (mais ayant des définitions différentes) et dont les auteurs font usage selon leurs préférences :
Ei(x), ei(x), En(x), E1(x), Ein(x)

JJa,

Je n'ai pas pris la peine de détailler les calculs mais j'ai bien pris comme définition .
Pour lui donner un sens quand x > 0 il faut effectivement l'interpréter par .
On obtient après calculs: qui est la formule que j'ai donnée.

Bonjour jandri,

mon message du 21-05-09 à 12:41 ne concernait pas la remarque tout à fait justifiée que tu as faite et que je n'ai pas contestée, bien au contraire : merci d'avoir fait la rectification.
L'information que j'ai ajoutée est d'ordre général, pour attirer l'attention sur les multiples variantes de fonctions apparentées que l'on rencontre selon les auteurs.
C'était aussi pour préciser que la définition classique de Ei(x) est une intégrale de Cauchy. Je suis bien d'accord : cette définition n'est pas d'un niveau élémentaire et je comprends pourquoi tu as préféré utiliser une formule plus accessible du point de vue pédagogique.

mais pourtant si on dérive -x²exp(1/x) on retrouve bien exp(1/x) non ?

donc -x²exp(1/x) serait une primitive de exp(1/x).

Non car la dérivée de -x²exp(1/x) n'est pas exp(1/x).
La dérivée de  -x²exp(1/x) est (1-2x)exp(1/x)