Inscription / Connexion Nouveau Sujet
représentation graphique d'une fonction impaire et périodique
Bonjour. Je ne sais pas comment faire pour représenter cette fonction.
Pourriez-vous m'aider à comprendre comment définir les points pour représenter f avec une période 2.
Merci.
Voici l'énoncé :
Une fonction f est impaire et périodique de période 2 ; donner une représentation graphique de f sur l'intervalle [-1,5].
Je sais que : f(x) = 1/x définie sur
 - {0} =
- {0} =  *
*
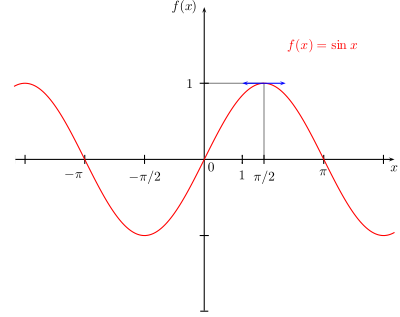
Chaque fois que x 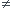 0,
0,
on a -x 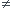 0 donc la première condition est réalisée :f(-x) = 1/-x = - 1/x = -f(x) ; f est donc impaire.
0 donc la première condition est réalisée :f(-x) = 1/-x = - 1/x = -f(x) ; f est donc impaire.
Et aussi que f impaire signifie que les points d'abscisse x et -x ont des ordonnées opposées ; l'origine du repère est donc centre de symétrie de la courbe.
Bonsoir. Tu connais la courbe qui représente f(x) = sin(x) ?
C'est une fonction périodique, et impaire ...
Quelle est ta fonction ?...elle pourrait ressembler à celle-là, en changeant la période ?...
Bonjour jacqlouis
Je fais une remise en math pour adulte par l'AFPA. Je n'ai pas encore abordé la fonction sin(x). Le livret sur lequel je travaille en ce moment ne traite que des généralités des fonctions.
Bonjour,
Une fonction est t-périodique (de période t) si et seulement sit
Par exemple la fonction sinus: f(x)=sin(x) a pour période

OK. Bien vu. Tu vas envisager la fonction " bordure de jardin " !...dont la courbe est un demi-cercle.
A partir de 0, dans ton repère , trace un demi-cercle le long de Ox , tourné vers les y positifs, un autre à la suite , et encore un quart de cercle.
Le 1er arceau va de x = 0 à x = 2, le 2ème de x=2 à x=4, le bout du 3ème de x= 4 à x= 5.
A partir de O, vers les x négatifs, tu traces un quart de cercle retourné cette fois vers le bas. L'abcisse de ce morceau va de x = 0 à x = -1 .
(désolé, je dois m'absenter 90 mn)...
Je retrouve Bluebird... On t'a envoyé cette courbe sinusoïdale que tu ne connais pas, et qui ne répond pas trop à ta question...
La courbe que je te proposais (l'as-tu dessinée ?) est simplement périodique, c'est-à-dire qu'on la retrouve identique toutes les 2 unités :
ce qui s'écrit : f(x) = f(x+2) = f(x +4) = ... f(x + 2*n ) ... cela pour expliquer qu'elle est périodique.
Mais elle est également impaire, car symétrique par rapport à l'origine (c'est-à-dire que si tu découpes la partie à droite de O, et que tu la fais pivoter autour de 0 d'un demi-tour, tu retrouves la même courbe , mais " la tête en bas "...).
Oui je suis entrain de la dessiner à la main.
J'ai un chercher sur le web s'il y avait un logiciel gratuit pour tracer les fonctions.
En fait ce que j'ai fait ressemble à cette courbe sinuoïdale.
Je vais scaner mon dessin et l'envoyer.
Merci beaucoup.
Si on demande courbe - impaire- période 2 - c'est inutile de la faire " vibrer " ou " onduler " autour de l'axe horizontal , comme la sinusoïde . Il suffit de la tracer au-dessus de 0x à droite, et en-dessous à gauche.
Il est parfait... On retrouve bien la fonction impaire (la courbe de O à -1 est identique à la courbe de 0 à +1, avec le signe opposé), et on voit que la courbe de 2 à 4 (et plus loin) est identique (superposable) à la courbe de O à 2.
Le morceau de 0 à 2 pourrait avoir n'importe quelle forme (demi cercle, comme je t'avais dit, ou triangle, ou courbe alternative comme le sinus ...) . Chaque morceau n'a même pas besoin d'être symétrique comme tu l'as fait : ce n'est pas faux, mais non obligatoire...
NON, ce n'est pas correct.
Cette fonction n'est pas périodique de période 2.

Exemple, les 2 points rouges écartés de 2 dans les abscisses DOIVENT avoir une même ordonnée.

Aucun des dessins fait jusqu'ici ne convient.
En voici un qui convient (il en existe évidemment une infinité d'autres).

Il faut quant même remarquer que f(x) existe sur R mais qu'on ne l'a représenté que sur [-1 ; 5].
Sauf distraction.








