Inscription / Connexion Nouveau Sujet
Sev, supplémentaires, matrice, symétrie et projection
Bonjour,
J'ai cet exercice que je n'arrive pas à terminer :
1) Soit F le sev de 
3, défini par F = { ( 2 y -z , y, z )} déterminer la dimension de F
2) Soit w = (1,1,2) montrer que F et G = vect (w) sont supplémentaires.
3) Déterminer dans la base canonique la matrice A de la projection sur F parallèlement à G, celle de la
projection sur G parallèlement à F et celle de la symétrie par rapport à F de direction G.
4)Déterminer une matrice diagonale semblable à A, puis calculer An
1) dimF=2 car la 1ère coordonnée est combinaison linéaire des deux autres.
2) Soient G=Vect(w)=Vect(1,1,2) et F=Vect((2,1,0),(-1,0,1))
F
G=3
dimF+dimG=3 et F
G={0}
dimF=2 et dimG=1, c'est donc vérifié.
Soit X=, X
FG
XG X=
d'où X=
XF, X=
FG={0} donc F et G sont supplémentaires.
2) A=PBP-1
B=P-1AP
rgA=3 Imf=Vect((1,1,2),(2,1,0),(-1,0,1))
Je n'ai pas fait attention mais nous en sommes donc à la question 3. 
Donc y serait le vecteur directeur de F et z celui de G ou j'ai mal compris ?
Ah d'accord, je comprends mieux, je cherchais le rapport avec la suite de mon exercice en fait. Merci à vous deux !
Mais du coup, j'ai A mais je ne sais pas comment répondre à "a projection sur F parallèlement à G, celle de la projection sur G parallèlement à F et celle de la symétrie par rapport à F de direction G. "
En gros, le premier vecteur de A serait la projection sur F//G, le second celui de la projection sur G//F et le dernier celui de la symétrie par rapport à F de direction G ?
3) La projection sur F parallèlement à G:
ce vecteur se compose de
avec
et
Soit la projection de
sur
parallèlement à
Donc est colinéaire à
d'où la relation
Avec donc vérifie l'équation du plan ce qui permet de déterminer
qu'on injecte dans le système d'équations pour calculer
en fonction de
ainsi on aura la matrice.
L'équation de ton plan F peut s'écrire
donc
d'où
Donc: que nous injectons dans le système d'équations
que nous écrivons sous la forme et vous obtenez votre matrice
.
L'équation de ton plan F peut s'écrire
Donc:
que nous écrivons sous la forme
Si j'ai bien compris - chose dont je doute -, il suffit que j'injecte
.
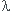Razes:
il y a une erreur de signe dans le message du 11-04-16 à 00:47: de
on tire x' = x - lambda... etc... et quand on transfert cà dans l'équation du plan,cà change la matrice à la fin. D'ailleurs si on vérifie, avec w1=(2,1,0),w2=(-1,0,1)) et w3=(1,1,2) on doit avoir Aw1 = w1, Aw2 = w2 (ok pour eux) mais Aw3 = 0 ce qui n'est pas le cas.
La matrice de la projection sur F parallèlement à G dans la base canonique de R^3 est A=
0 2 -1
-1 3 -1
-2 4 -1
ListenAicha:
Pour calculer celle de la projection sur G // à F on peut faire A' = I - A, au lieu de faire tous les calculs pour ce cas. On peut trouver cette formule en faisant un dessin.
Et pour la matrice S de la symétrie par rapport à F de direction G: elle laisse les vecteurs de F inchangés et inverse le signe de ceux de G: Sw1 = w1, Sw2 = w2 et Sw3 = -w3. Pour la calculer on peut se servir de la projection sur F // G (matrice A): c'est S = 2A - I. On peut aussi trouver cette formule en faisant un dessin.
Toutes ces matrices peuvent aussi être calculées en utilisant la formule de changement de base.
J'ai énormément du mal à visualiser tout ça.
Pour moi, l'énonce me laissait penser qu'il n'y avait qu'une matrice A, commune aux 2 projections et à la symétrie.
Donc ce serait cela ?
Chaque projection a sa propre matrice. Pour ce qui est du calcul, je n'ai pas vérifié. J'ai essayé de vous montrer le principe du calcul.
D'accord, merci !
Bon, du coup, pour les matrices semblables à A, A' et S, j'utilise la relation avec la matrice de passage pour les déterminer :
A=PAsemblableP-1Asemblable=P-1AP
A'=PA'semblableP-1A'semblable=P-1A'P
S=PS'semblableP-1Ssemblable=P-1SP
Est-ce bien cela ?
Oui. Mais attention c'est A' = I - A =
1 -2 1
1 -2 1
2 -4 2
Soit B la matrice semblable à A dans la base (w1,w2,w3) avec w1,w2 vecteurs de F et w3 vecteur de G. Alors B=
1 0 0
0 1 0
0 0 0
car on doit avoir Bw1=w1, Bw2=w2 et Bw3=0 (projection sur F parallelement à G). Donc A = P B P^-1.
De la même facon, la matrice de A' dans la base (w1,w2,w3) est B'=
0 0 0
0 0 0
0 0 1
car B'w1=0, B'w2=0, B'w3=1 (proj sur G // F), et A' = P B' P^-1
Mais comme je l'ai mentionné on peut faire plus intelligent. On remarque que B+B'=I donc B'=I-B et A'=P(I-B)P^-1 = PIP^-1 - PBP^-1 = I - A
Pour la symétrie, la matrice dans la base w1,w3,w3 est S'=
1 0 0
0 1 0
0 0 -1
car elle laisse w1,w2 inchangés et inverse le signe de w3. Donc S = PS'P^-1. Mais on remarque aussi que S' = B - B' donc S = P(B-B')P^-1 = PBP^-1 - PB'P^-1 = A - A' = A - (I-A) = 2A - I.
La question 4 est de trouver une matrice D diagonale pour calculer A^n. Puisque A est une projection, ses valeurs propres et vecteurs propres sont très faciles à trouver. Il reste à calculer A^n = P D^n P^-1, mais on remarque aussi que A^2 = A (ca peut même servir de définition d'une projection) donc A^3 = A^2 = A, etc. et A^n = A, qu'on peut prouver par récurrence. Donc calculer D^n est assez facile...
Mais comme je l'ai mentionné on peut faire plus intelligent. On remarque que B+B'=I donc B'=I-B et A'=P(I-B)P^-1 = PIP^-1 - PBP^-1 = I - A
Comment on est censé le remarquer ?
La question 4 est de trouver une matrice D diagonale pour calculer A^n. Puisque A est une projection, ses valeurs propres et vecteurs propres sont très faciles à trouver. Il reste à calculer A^n = P D^n P^-1, mais on remarque aussi que A^2 = A (ca peut même servir de définition d'une projection) donc A^3 = A^2 = A, etc. et A^n = A, qu'on peut prouver par récurrence. Donc calculer D^n est assez facile...
Comment faire sans les valeurs propres et vecteurs propres ? Ce n'est pas au programme de sup.
Comment on est censé le remarquer ?
C'est le b-a-ba des sous-espaces supplémentaires. Dire que
Comment on est censé le remarquer ?
C'est le b-a-ba des sous-espaces supplémentaires. Dire que
Bah oui, je suis bête, je n'avais pas pensé à cela.
, mon exercice n'étant pas résolu. Merci ! Ben c'est à toi à finir la résolution avec les éléments que tu as reçus, non ? On ne va pas le faire à ta place. Qu'est-ce qui te pose encore problème ?
Il vous reste:
4)Déterminer une matrice diagonale semblable à , puis calculer
Savez vous calculer la matrice diagonale?
Ben c'est à toi à finir la résolution avec les éléments que tu as reçus, non ? On ne va pas le faire à ta place. Qu'est-ce qui te pose encore problème ?
Recomic35, bien heureusement ! Sinon, j'aurai cherché la correction sur Internet.
sylvainc2 m'a expliquée comment trouver cette matrice diagonale en me parlant de valeurs propres, chose qui m'a plus que perturbée étant donné que c'est au programme de MP et non MPSI. De ce fait, j'ai demandé comment faire sans valeur propre et cette question est restée sans réponse.
Il vous reste:
4)Déterminer une matrice diagonale semblable à
Savez vous calculer la matrice diagonale?
Razes, que dois-je faire pour déterminer cette matrice diagonale ?Je me servirais bien de la relation avec la matrice de passage, l'inverse de cette dernière et A. Est-ce ce qu'il faut faire ?
Il n'y a pas besoin de valeur propre.
Tu as la matrice B de la projection dans la base formée d'une base de F et d'une base de G. Cette matrice B est diagonale, très simple, et semblable à A (la matrice de changement de base est donnée par les bases de F et G que tu as).
C'est vrai, la matrice B est semblable.
Mais sincèrement, faite un petit effort et calculer les valeurs propres, ce n'est pas difficile. Vous allez obtenir entre-autre la matrice B.
Il suffit de résoudre l'équation résultante de :
Pourquoi insister sur les valeurs propres alors que ça ne sert strictement à rien ici et que ce n'est pas au programme de la classe de ListenAicha ?
Soit B la matrice semblable à A dans la base (w1,w2,w3) avec w1,w2 vecteurs de F et w3 vecteur de G. Alors B=
1 0 0
0 1 0
0 0 0
car on doit avoir Bw1=w1, Bw2=w2 et Bw3=0 (projection sur F parallelement à G). Donc A = P B P^-1.
Si j'ai insisté, c'est qu'on dirait que ListenAicha n'a pas bien saisi votre argumentation.
1) Ce n'était pas mon argumentation.
2) Ce n'est pas en lui parlant de choses qu'il ne connaît pas qu'il saisira mieux.
Désolé, ce n'est pas votre argumentation, mais vous avez cité la matrice B et je ne sais pas si ListenAicha avait bien compris pourquoi B est semblable à A surtout avec des explications de changement de bases.
Je pense avoir compris.
Oui. Mais attention c'est A' = I - A =
1 -2 1
1 -2 1
2 -4 2
Soit B la matrice semblable à A dans la base (w1,w2,w3) avec w1,w2 vecteurs de F et w3 vecteur de G. Alors B=
1 0 0
0 1 0
0 0 0
car on doit avoir Bw1=w1, Bw2=w2 et Bw3=0 (projection sur F parallelement à G). Donc A = P B P^-1.
De la même facon, la matrice de A' dans la base (w1,w2,w3) est B'=
0 0 0
0 0 0
0 0 1
car B'w1=0, B'w2=0, B'w3=1 (proj sur G // F), et A' = P B' P^-1
Mais comme je l'ai mentionné on peut faire plus intelligent. On remarque que B+B'=I donc B'=I-B et A'=P(I-B)P^-1 = PIP^-1 - PBP^-1 = I - A
Pour la symétrie, la matrice dans la base w1,w3,w3 est S'=
1 0 0
0 1 0
0 0 -1
car elle laisse w1,w2 inchangés et inverse le signe de w3. Donc S = PS'P^-1. Mais on remarque aussi que S' = B - B' donc S = P(B-B')P^-1 = PBP^-1 - PB'P^-1 = A - A' = A - (I-A) = 2A - I.
La question 4 est de trouver une matrice D diagonale pour calculer A^n. Puisque A est une projection, ses valeurs propres et vecteurs propres sont très faciles à trouver. Il reste à calculer A^n = P D^n P^-1, mais on remarque aussi que A^2 = A (ca peut même servir de définition d'une projection) donc A^3 = A^2 = A, etc. et A^n = A, qu'on peut prouver par récurrence. Donc calculer D^n est assez facile...
En fait, les matrices semblables et diagonales sont :
-
-
-
Du coup, on a aisément Dn et grâce à la formule de passage An, A'n et S'n.
D'ailleurs, ça me perturbe parce que l'énoncé semble sous-entendre qu'A est unique.
D'ailleurs, ça me perturbe parce que l'énoncé semble sous-entendre qu'A est unique.
La matrice
3) Déterminer dans la base canonique la matrice A de la projection sur F parallèlement à G, celle de la
projection sur G parallèlement à F et celle de la symétrie par rapport à F de direction G.
D'ailleurs, ça me perturbe parce que l'énoncé semble sous-entendre qu'A est unique.
La matrice
Je suis vraiment perdue. Parce qu'en fait, A c'est simplement celle de la projection sur F//G. Donc je dois ignorer A' (projection G//F et la symétrie) ?
B est semblable à A mais ne la remplace pas. Chacune des matrices semblables représente la même transformation mais dans deux bases différentes.
A dans la base mais B dans la base
Avec
Je pense avoir enfin compris
On demande juste une matrice diagonale, semblable à la projection de F//G, celle qu'on a noté A. Les projections de G//F et la symétrie n'étaient là que pour la question 3).
Merci beaucoup ! 
On sait que
On remarque D=D2=D3...
Par récurrence, on voit clairement que
On a :
det P=-1 donc P est inversible. J'ai trouvé comme inverse
Sauf erreur de calcul.
Non. Tu dois avoir pour tout entier
.
Pour montrer ça, il est plus simple de vérifier que A^2=A que de passer par le changement de base !
L'intitulé de la question laissait penser qu'il fallait se servir de .
Du coup, on a bien . Il faut que je valide par récurrence ?
Pour le passage par la matrice :
On sait que et il est évident que
pour tout entier
.
On en déduit que pour tout entier
.
Ca se démontre aussi par récurrence à partir de .
On fait comme on veut. La façon dont est écrit l'énoncé pousse à la première démarche.
Annuler
connectez vous
algèbre en post-bac