Bonsoir,

Ta fonction f4 peut s'écrire f4 = a o f avec a(x) = -3x+2 ( fonction affine décroissante sur R)

Tu appliques donc les règles de variation d'une fonction composée pour faire ton tableau.
Pour les valeurs de f4(x) tu peux tout à fait utiliser f4(x) = 2-3f(x).

Merci beaucoup !
Au fait, voici le tableau de variation d'origine ci-dessous, j'avais oublié de vous le donner =S

Et j'ai donc trouvé, pour le tableau de variation de -3x+2 :
f(-5)+2 = 1/2 + 2 = 5/2
et f(3)+2 = -1/3 + 2 = 5/3

Par contre, on ne peut pas trouver d'image pour -1, comme c'est une valeur interdite, si ?

Merci encore

pour le tableau de variation de f tu as:

sur [-5;-1[ , f est croissante à valeurs dans [1/2;+inf[
a est décroissante sur [1/2;+inf[
donc f4 est décroissante sur [-5;-1[

sur]-1;3], f est décroissante à valeurs dans ]+inf;-1/3]
a est décroissante sur ]+inf;-1/3]
donc f4 est croissante sur ]-1;3]

et f4(-3) = 2-3*(1/2) = 1/2
f4(3) = 2-3*(-1/3)= 3

et effectivement tu n'as pas l'image de -1.

euh il manque le 4 dans la première phrase... c'est le tableau de variation de f4 bien sûr...

et f4(-3) = 2-3*(1/2) = 1/2
f4(3) = 2-3*(-1/3)= 3

Je n'ai pas compris ce passage, pourquoi ne garde t-on pas -5 et 3 ? Cette fonction est de la forme u(x)+k, donc pour trouver f4 il faut réaliser une translation de vecteur k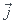, où k = 2 ? donc ce ne sont pas les images qui changent, mais les ordonnées ?

ben... parce que j'ai fait une faute de frappe lol et en fait j'ai bien calculé l'image de -5 qui est 1/2

Okai, désolé x)
Mais alors du coup pour calculer l'image on ne prend pas la forme : 3x+2
mais la forme 2-3f(x) ?

non non, ne confonds pas :
a(x) = -3x+2
et f4(x) = a(f(x)) = -3f(x)+2 ou encore 2-3f(x), c'est pareil.

Okai, merci bien!

de rien!

Pardon de vous déranger encore une fois, mais il y a encore une petite question que j'aimerai vous poser
il y a une fonction, c'est f2 : x f(x+2)
Je sais que cette fonction est de la forme u(x+k), où k=2
Et la courbe de cette fonction est la translation de f par le vecteur -k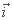, donc ici -2.
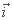Donc là, pour le tableau de variation, ce sont les abscisses qui bougent, car on translate vers la gauche.
Mais comment fait-on pour calculer les images, on part aussi de f(-5) et f(3) ? ou de f(-7) et f(1) ?

Merci après je ne vous embête plus ^^

Bonjour,

Tu ne m'embêtes pas , mais normalement nouveau sujet => nouveau topic!
Exceptionnellement et comme c'est le même thème, je réponds ici...
Pour calculer ces images:
f2(-5) = f(-5+2) = f(-3)
f2(3) = f(3+2) = f(5)
f2(-7) = f(-7+2) = f(-5)
f2(1) = f(1+2) = f(3)
et tu te sers de ce que tu connais sur f pour les réponses ( tableau de variation ou formule)

Mais comme cette courbe subit une translation de vecteur -2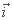, du coup les abscisses changent, mais pas les ordonnées. Donc on garde les ordonnées de la fonction d'origine ?

mais si tu déplaces la fonction à l'horizontale regarde ce qui se passe:


je prends la fonction
f(x) = x²
g(x) = f(x-1) = (x-1)²



tu as g(1) = f(0)et non pas f(1), non?

Oui, c'est vrai mais alors je n'ai toujours pas compris comment on calcule les abscisses et les ordonnées de f(x) = f(x+2) ...

(Je suis longue a la compréhension désolé -_-)

euh non attention on n'a pas f(x) = f(x+2)

tu sais que f₂ : x f(x+2)

tu as donc f₂(x) = f(x+2) ne confonds pas f₂ et f.

pour trouver l'image d'un nombre x par f₂, tu vas chercher l'image qu'avait x+2 par f , puisque en se décalant à gauche de 2 unités on arrive sur la courbe de f.

par exemple pour avoir l'image de 1 par f₂ , tu vas prendre l'image de 1+2 par f
donc f₂(1) = f(1+2) = f(3) = ...

tu vois?

Mais déjà comme c'est de la forme u(x+k) et bien le vecteur de translation est bien de -2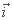 donc il ne faut pas chercher l'image qu'avait x-2 ?
et même, comment on peut trouver l'image de 3, on ne l'a pas ? enfin je ne comprend pas

non quand tu as un translation de vecteur i tu as : f2(x) = f(x2)

prends un papier et un crayon, dessine une courbe quelconque de f
decale la à gauche de 2 unites et tu as celle de f2
maintennat cherche l'image de x avec f2 tu verras que c'est la meme que l'image de x2
avec f.

pour l'image de 3 , il me semble que ton tableau te donne f(3) = -1/3 non?

Ok donc après ça me ramène bien à
f2(-5) = f(-5+2) = f(-3)
f2(3) = f(3+2) = f(5)

Comme vous l'aviez dit mais l'image de -3 et celle de 5 ... on ne les a pas

eh bien on laisse les valeurs f(-3) et f(5) dans le tableau , sans les resultats.

Donc par exemple si on prend le tableau je met f(-3) à la place de 1/2 ? et pour ce qui est des x, je laisse -5, -1 et 3 ? je met pas -7, -3 et 1 ? comme on décale la courbe à gauche de 2unites.

lol bon je crois que depuis qu'on fait ce sujet on finit par tout mélanger ... moi la premiere !!

quand tu m'as posé la question du calcul d'images je n'ai pas tilté sur le fait que c'était pour construire au depart le tableau de variation, puis je suis restée sur l'idée de -5 et 3...

bien sûr qu'ici le tableau de f2 fait apparaitre: -7...-3...1 puisqu'on est décalé
on aura à placer donc
f2(-7)= f(-5) = 1/2
f2(-3) qui n'existe pas car -3 est valeur interdite
f2(1)= f(3)= -1/3

mieux?

Dernière petite question : on garde f(-7) = 1/2 car les images ne sont pas décalées ?

oui , elles ne sont pas decalees en hauteur c'est juste une translation horizontale.

attention c'est (-7) = 1/2 et non pas f(-7)

puisque f2(-7) = f(-7+2) = f(-5)= 1/2

mais on l'a déjà dit ...

Ok oui j'oublie toujours le 2 -_-
Merci beaucoup, bon là je vais finir seule, mais merci encore =)

de rien! bonne continuation !