Bonjour,
Pour pouvoir vous répondre, il faudrait que vous précisiez en détail ce qu'est pour vous une distribution normale.
Concernant le test du Khi2 il est surtout utilisé pour comparer une certaine distribution à une distribution type, c'est à dire de référence.
Cordialement.

Une distribution normale, selon mon entendement, est une distribution de probabilités
d'une variable aléatoire continue dont la courbe est parfaitement symétrique et en forme de cloche (cf. fig. ci-jointe). Ma question est relative à la courbe en rouge et à la possibilité de calculer un intervalle de confiance y relatif.

Bonne soirée et merci pour votre patience.

Oui, mais, à mon avis, vous oubliez une chose importante, la symétrie de la courbe se fait par rapport à la moyenne.
Donc si la moyenne des ages est 25 ans par exemple, le nombre par tranche d'age, par rapport à 25 sera symétrique et dans des proportions normales.
Rien ne dit que la répartition des ages des membres du forum n'est pas conforme à la loi normale, sauf peut-être votre seconde courbe, si c'est ça dont il s'agit.
Si on suppose qu'il y a en gros, 2 types de membres, ceux qui posent des questions et ceux qui répondent (je simplifie volontairement), alors il n'y a aucune raison que la répartition soit conforme à la loi normale, puisqu'on peut supposer que ceux qui posent des questions sont plus jeunes et plus nombreux que ceux qui répondent
Si vous faites la répartition par rapport à leur taille (en l'occurrence inconnue), là vous aurez bien un test aléatoire.  
Dans un sens vous avez raison : un test de khi2 ne convient pas pour vérifier une répartition telle que l'age des membres.

De ce dont je me souviens, le test du Khi-deux sert à:

- soit comparer une distribution observée par rapport à une distribution théorique suivant une loi de probabilité quelconque (pas forcément normale)
- soit comparer deux distributions observées pour voir si elles suivent ou non la même loi (pas forcément normale).

Au contraire de l'ANOVA, le Khi-deux n'a pas à vérifier les conditions de normalité. Il y a parcontre d'autres conditions à vérifier pour que le test soit valable.

Bonsoir,
un petit rappel :
Dlzlogic est célèbre sur de nombreux forums de maths pour son incompétence en probabilité et statistique.

Pour la question de Debuttemps il faudrait préciser ce que tu veux tester avec un 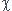².

...Euh, moi aussi, c'est la raison pour laquelle je suis ici...

Bref, je voudrais connaitre la manière de calculer un intervalle de confiance sur une telle distribution. Dans le cas d'une distribution normale, c'est très facile, notamment avec excel. Avec ce genre de distribution, il est patent que la formule standard n'est pas appropriée.

Un intervalle de confiance par rapport à quoi ?

Je ne sais toujours pas ce que tu veux calculer : un intervalle de confiance ok, mais de quoi ?

Au passage si tu as une idée sur la forme de la densité, par exemple la densité suit une loi bêta, tu peux essayer de donner un intervalle de confiance pour les paramètres.

Mais là je suis à la limite de mes compétences.

J'ai une série de données qui sont distribuées selon une courbe log normale. Je souhaite connaitre l'intervalle de confiance (1-) d'une moyenne de population (valeurs ) qui m'assure à 95% d'être entre les fameuses bornes à gauche et à droite (/2).

Si tu connais la loi, il n'y a pas de difficultés théoriques.
C'est juste du calcul. Pas toujours facile.

@ Debuttemps,
Ecoutez plutôt les conseils de nombrilist.
A part "j'y connais rien" verdurin n'a rien dit d'utile.

Bonsoir
oh que si, il a dit des choses utiles.... qui ont aidé à comprendre comment quelqu'un qui n'a apparemment jamais entendu parler de loi normale se trouve être le premier à répondre à un sujet où il en est un peu question !