Bonjour Dpi,

Pour ce premier tour des primaires,
je vous propose mon candidat.

Bonjour caylus,

Merci pour la candidature,à priori
candidat obtus et penchant à gauche

Bonjour

Sur une feuille de papier, j'ai tracé au stylo un trait quelconque, représentant la base d'un triangle.
Puis, j'ai tracé les traits correspondant à tout les points possible pour que le triangle soit rectangle, ou isocèle.

Ça donne ça :

 Cliquez pour afficher

Désolé pour la qualité de l'image, je n'avais ni règle ni compas. J'ai du faire avec le peu de moyen à ma disposition, notamment pour prendre la photo ( en effet, ce n'est pas un scann ^^' )

 Cliquez pour afficher

Encore une fois, je ne me félicite pas pour la qualité des images

Bonjour

à Anthony

Ton approche par zone est intéressante

J'aime bien ton z2.

A tous

Le shéma d'Anthony définit les lignes et les zones
qui permettront de choisir le point C "idéal"

Peut être que le nombre d'or donnerait une indication ?
De toute façon ce seront des angles que nous retiendrons.

Bonjour Dpi.

 Cliquez pour afficher

Le triangle dont les angles sont aigus et diffèrent le plus possible entre eux et de 90 degrés a peut-être des angles de 75, 60 et 45 degrés.
En posant le plus grand côté égal à 1 et h sa hauteur :
h(1 + 1/√3) = 1; h = √3/(√3+1)
L'un des côtés mesure √3*√2/(√3+1) = √6/(√3+1) environ 0,9.
Le dernier côté mesure : (2/√3)*(√3/(√3+1) = 2/(√3+1) environ 0,73.
Ce triangle est formé de deux triangles rectangles, dont l'un est isocèle et l'autre est la moitié d'un triangle équilatéral. On peut le représenter avec les deux modèles d'équerres.

Bonjour,

à plumemeteore

 Cliquez pour afficher

Ce qu'il y a de bien c'est que l'approche esthétique
peut s'appuyer sur un raisonnement mathématique ...

Dans notre cas j'ai une approche trés voisine:

1/on évitera un angle obtus ,l'angle moyen est 60°

2/si on prend  comme point de départ ,on peut dire:
90< Â <60 pourquoi pas 75°.

3/Utilisons le nombre d'or (pouquoi pas ?)
Si AB = 1 le nombre d'or donnerait AC+BC =(1+25 )/2
je trouve  B =42°56 et C=62°44

Curiosité ou évidence

En travaillant sur les angles de notre futur
triangle quelconque idéal,j'ai trouvé
qu'un triangle isocèle avec deux angles de 36°
et deux cotés égaux à 1 avait une base égale
au nombre d'or.

Ce qui implique qu'un pentagone de coté 1
a aussi cette particularité pour ces "diagonales"
joignant deux cotés consécutifs

bonsoir,

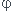est très présent dans le pentagone
si on coupe un pentagone avec deux diagonales partant du même sommet, on obtient un triangle 72°, 72°, 36° et deux triangles 36°, 36°, 108°

si on prend un triangle 72°, 72°, 36° et qu'on trace la bissectrice d'un angle de 72°, on obtient un nouveau triangle 72°, 72°, 36° et un triangle 36°, 36°, 108°

Bonjour

Les triangles sont à la mode (voir la dernière énigme)

Pour le moment il semblerait que les quelconques (ou scalènes)" idéaux" soient:

75 ° 60 ° 45 °     constructible à la règle et au compas
75 ° 62 °4  47°6   somme des deux petits cotés /base =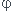

Mais nos experts en géométrie n'ont pas encore planché...

Bonsoir, je ne suis vraiment pas un expert en géométrie.

Je me permet néanmoins de remarquer que, dans la construction d'Anthony, on peut se limiter à considérer les zones 3 et 4, à une similitude près.
J'ai lu, il y a fort longtemps, un article sur ce thème dans le bulletin de l'APMEP.
Mais je ne l'ai plus et je ne me souvient pas de la méthode utilisée pour trouver le point le plus loin possible des bords. J'ai fait quelques tentatives, sans rien trouver de concluant.

Une autre approche : on sait que, dans un triangle équilatéral, la somme des distances d'un point intérieur au triangle avec les cotés est constante (c'est la hauteur du triangle).
On prend un triangle équilatéral de hauteur 180°.
Chaque point intérieur représente un triangle, et tous les triangles sont représentés, à une similitude près.

Le triangle ap,bp,cp correspond aux triangles rectangles.
Les segments a,ap ; b,bp et c,cp aux triangles isocèles. Le point g correspond au triangle équilatéral.
Compte tenu des symétries évidentes, on peut se limiter à ce qui se passe dans le triangle a,cp,g.
Les triangles acutangles sont représentés par un point dans h,cp,g et les triangles obtusangles par un point dans a,cp,h.

Comme point le plus loin des côtés d'un triangle, je propose le centre du cercle inscrit.

Ce qui conduit a
--pour un triangle acutangle à des angles de 41°(environ) 60°(exactement) 79°(environ)
--pour un triangle obtusangle 19°(environ) 52°(environ) 109°(environ)

Bonjour verdurin

Comme nous nous intéressons de préférence aux triangles acutangles
nous retenons 41,60,79°

Nous voyons que nos 3 candidats actuels sont très proches.

Je propose donc d'attendre une 4e candidature et de faire une
simple moyenne arithmétique car un vote serait fastidieux

Bonjour à tous,

Comme l'a dit Verdurin il y a eu un article sur le thème du triangle quelconque dans un bulletin de l'APMEP, précisément le bulletin 347 de février 1985 (page 103) avec une suite dans le bulletin 351 de décembre 1985 (page 911).
Ces deux articles ont été rédigés par Jacques Lubczanski.
Il obtient plusieurs triangles dont le triangle 45°,60°,75°.

Par chance on peut accéder à un article reprenant tout sur le site de l'APMEP.
Voici la référence:

Bonjour à tous,

Ce que vous cherchez n'existe pas.
Car si un triangle était LE triangle quelconque idéal, par définition il ne serait plus quelconque...

à jandri

Merci.

J'ai fait Monsieur Jourdain.
C'est exactement le fruit de ma réflexion initiale

à frenicle

Dès mon introduction ,je disais la difficulté à ne
pas tomber sur des particularités ..

D'où mon idée d'accoler les termes quelconques et "idéaux"
Le site donné par jandri et le thème annoncé par verdurin
répondent donc parfaitement.

A noter que les participants ont eu d'excellentes idées